Во времена Исаака Ньютона под функцией понимали некоторую аналитическую
формулу типа
Более общее определение предложили Е.Дирихле и А.И.Лобачевский. При этом
основным неопределяемым понятием принимается понятие соответствия: ![]() .
.
Например, между элементами множества ![]() и элементами множества
и элементами множества ![]() установлено
соответствие
установлено
соответствие ![]() . Причем не всем элементам из
. Причем не всем элементам из ![]() поставлены в соответствие элементы из
поставлены в соответствие элементы из
![]() , не все элементы из
, не все элементы из ![]() поставлены в соответствие элементам из
поставлены в соответствие элементам из ![]() , и соответствие
неоднозначно (см. рис. 5.1.1, 5.1.2).
, и соответствие
неоднозначно (см. рис. 5.1.1, 5.1.2).
Соответствие ![]() между элементами множеств
между элементами множеств ![]() и
и ![]() называется
функцией, если любому элементу
называется
функцией, если любому элементу ![]() поставлен в соответствие единственный элемент
поставлен в соответствие единственный элемент ![]() (это записывается следующим образом:
(это записывается следующим образом: ![]() или
или
![]() ).
).
Приняты следующие определения и обозначения:
![]() -- область определения функции
-- область определения функции ![]() ;
;
![]() -- область значений функции
-- область значений функции ![]() ;
;
![]() -- полный образ множества
-- полный образ множества ![]() при отображении
при отображении ![]() , или множество значений функции
, или множество значений функции ![]() ;
;
![]() -- прообраз элемента
-- прообраз элемента ![]() при данном соответствии
при данном соответствии ![]() ;
;
![]() -- образ элемента
-- образ элемента ![]() ;
;
![]() -- полный прообраз элемента
-- полный прообраз элемента ![]() .
.
При помощи соответствия можно задать, например, такую сложно устроенную
функцию:
Соответствие, задаваемое функцией, удобно изображать в
виде
графика:
![]() .
.
В курсе математического анализа в основном рассматриваются числовые функции, т. е.
такие, что
![]() .
.
1) ![]() сюръективна (отображает
сюръективна (отображает ![]() на
на ![]() ), если
), если
![]() (или, что то же самое:
(или, что то же самое:
![]() ),
см. рис. 5.1.3;
),
см. рис. 5.1.3;
2) ![]() инъективна, если различные элементы из
инъективна, если различные элементы из ![]() имеют различные образы в
имеют различные образы в ![]() (см. рис. 5.1.4);
(см. рис. 5.1.4);
3) ![]() биективна или взаимно однозначна, если функция
биективна или взаимно однозначна, если функция ![]() сюръективна и инъективна (см. рис. 5.1.5);
сюръективна и инъективна (см. рис. 5.1.5);
Пусть даны две функции ![]() и
и ![]() . Функция
. Функция ![]() ,
определяемая равенством
,
определяемая равенством
![]() , называется
сложной функцией (или
суперпозицией функций) от
, называется
сложной функцией (или
суперпозицией функций) от ![]() и
и ![]() .
.
Пример 5.1.1.
![]() . Тогда
. Тогда
![]() ,
,
![]() .
.
Ясно, что, вообще говоря,
![]() .
.
Если определена функция ![]() , которая есть наложение на
, которая есть наложение на ![]() , то на
, то на ![]() определено
соответствие
определено
соответствие
![]() . Это соответствие будет функцией, если оно однозначно,
т. е. для любого
. Это соответствие будет функцией, если оно однозначно,
т. е. для любого
![]() состоит из одного и только одного элемента. В таком
случае эта функция называется обратной функцией к функции
состоит из одного и только одного элемента. В таком
случае эта функция называется обратной функцией к функции ![]() и обозначается
и обозначается
![]() , или
, или ![]() .
.
Пример 5.1.2. Пусть
![]() . Тогда
. Тогда
![]()
Определение предела функции по Гейне. Пусть в каждой точке интервала ![]() ,
кроме, быть может, точки
,
кроме, быть может, точки ![]() , определена функция
, определена функция ![]() (см. рис. 5.2.1).
(см. рис. 5.2.1).
Число ![]() называется пределом функции
называется пределом функции ![]() при стремлении
при стремлении ![]() к
к ![]() , если для
любой последовательности
, если для
любой последовательности
![]() такой, что
такой, что
Пример 5.2.1. Пусть
Пример 5.2.2. Пусть
Определение предела функции по Коши.
Пусть в каждой точке интервала
Теорема 5.2.1. Определения предела функции по Гейне и по Коши
эквивалентны
Доказательство.
Пусть
Достаточность. Пусть
Согласно определению Гейне, возьмем любую последовательность
Пример 5.2.3.
Докажем, что по определению Коши
Возьмем произвольное
Пример 5.2.4.
Докажем, что по определению Коши
Говорят, что функция ![]() , кроме,
быть может, точки
, кроме,
быть может, точки ![]() , определена функция
, определена функция ![]() (см. рис. 5.2.2). Число
(см. рис. 5.2.2). Число ![]() называется пределом функции
называется пределом функции ![]() при стремлении
при стремлении ![]() к
к ![]() , если для любого
, если для любого
![]() существует
существует
![]() такое, что для всех
такое, что для всех ![]() , удовлетворяющих условию
, удовлетворяющих условию
![]() , выполняется неравенство
, выполняется неравенство
![]() . Или, на формальном языке,
. Или, на формальном языке,
![]()
![]()
Необходимость. Докажем от противного. Пусть
![]() по Гейне, но не по Коши, т. е.
по Гейне, но не по Коши, т. е.
![]()
![]()
![]() . Тогда по (5.2.2) найдутся
. Тогда по (5.2.2) найдутся ![]()
![]() и
и
![]() . Отсюда
. Отсюда
![]() , и по свойству (3.2.5)
, и по свойству (3.2.5) ![]() . Поэтому, по определению Гейне,
. Поэтому, по определению Гейне,
![]() , но по построению последовательность
, но по построению последовательность
![]() лежит вне
окрестности
лежит вне
окрестности
![]() , что противоречит тому, что
, что противоречит тому, что ![]() .
.
![]() (по Коши).
(по Коши).
![]() . Для доказательства того, что
. Для доказательства того, что ![]() ,
возьмем любое
,
возьмем любое
![]() . Тогда из определения предела по Коши найдется соответствующее
. Тогда из определения предела по Коши найдется соответствующее
![]() . Для
. Для ![]() , в силу сходимости
, в силу сходимости ![]() , найдется номер
, найдется номер
![]() такой, что для всех
такой, что для всех
![]() , но тогда по определению Коши
, но тогда по определению Коши
![]() , что доказывает, что
, что доказывает, что ![]() , т. е.
, т. е.
![]() (по Гейне).
(по Гейне).
![]()
![]() , рассмотрим левую часть основного неравенства
в определении Коши (5.2.1)
, рассмотрим левую часть основного неравенства
в определении Коши (5.2.1)
![\begin{eqnarray*}
\vert f(x)-A\vert & = & \vert x^2-4\vert=\vert x-2\vert\vert x...
...$,\\ тогда $1<x<3$}\right] \le\vert x-2\vert(3+2)<\varepsilon ,
\end{eqnarray*}](../img/img636.gif)
поэтому
![]() Искомое
Искомое
![]() . Здесь
. Здесь
![]() и
и
![]() Действительно, пусть для всех
Действительно, пусть для всех ![]() выполняется
выполняется
![]() , тогда
, тогда
![]() , поэтому
, поэтому
![]()
![]()
Возьмем произвольное
![]() , рассмотрим
, рассмотрим
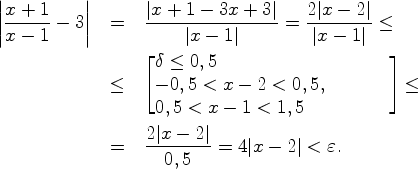
Искомое
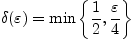 .
.
![]() удовлетворяет
условию Коши в точке
удовлетворяет
условию Коши в точке ![]() , если она
определена в
, если она
определена в ![]() , быть может, кроме самой точки
, быть может, кроме самой точки ![]() , и выполнено
, и выполнено
![]()
![]()
Теорема 5.3.1. Для того чтобы существовал конечный предел
![]() необходимо и достаточно, чтобы в точке
необходимо и достаточно, чтобы в точке ![]() выполнялось условие Коши для
функции
выполнялось условие Коши для
функции ![]()
Доказательство.
Необходимость. легко следует из
определения предела по Коши (5.2.1). Действительно, возьмем любое
![]() , тогда по
(5.2.1) для
, тогда по
(5.2.1) для
![]() найдется
найдется
![]() . Возьмем любые
. Возьмем любые
![]() , тогда
, тогда
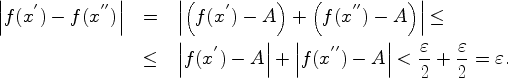
Достаточность. Пусть выполняется условие (5.3.1). Докажем, что существует
Пример 5.3.1.
Докажем, что не существует
Функции могут быть заданы на интервалах, примыкающих к точке ![]() , разными формулами
либо не определены на одном из интервалов. Для исследования поведения таких функций
удобным является понятие левосторонних и правосторонних пределов.
, разными формулами
либо не определены на одном из интервалов. Для исследования поведения таких функций
удобным является понятие левосторонних и правосторонних пределов.
Пусть функция ![]() определена на интервале
определена на интервале ![]() . Число
. Число ![]() называется пределом функции
называется пределом функции ![]() слева в точке
слева в точке ![]() ,
,
Предел функции ![]() справа в точке
справа в точке ![]() определяется аналогично.
определяется аналогично.
Пример 5.4.1. Пусть
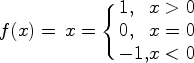
Ясно, что функция ![]() имеет предел в точке
имеет предел в точке ![]() тогда и только тогда, когда в этой
точке существуют пределы слева и справа для
тогда и только тогда, когда в этой
точке существуют пределы слева и справа для ![]() и они равны.
и они равны.
Если ![]() то
то
![]() определяется по Коши
следующим образом:
определяется по Коши
следующим образом:
Пример 5.4.2. Докажем, что
1. Арифметические свойства предела функции. Пусть функции ![]() и
и ![]() определены на
интервале
определены на
интервале ![]() , кроме, быть может, точки
, кроме, быть может, точки ![]() . Если существуют пределы
. Если существуют пределы
![\begin{eqnarray*}
\mbox{а)} && \lim_{x\to x_0}{\left[f(x)+g(x)\right]}= \lim_{x\...
...its_{x\to x_0}{g(x)}}}, \mbox{
если }\lim_{x\to x_0}{g(x)}\ne0.
\end{eqnarray*}](../img/img690.gif)
Эти свойства вытекают из определения Гейне предела функции и соответствующих свойств сходящихся последовательностей.
2. Если
Действительно, если взять
![]() , то из существования конечного предела следует, что существует
, то из существования конечного предела следует, что существует ![]() , что
для всех
, что
для всех ![]()
![]() , выполняется
, выполняется ![]() , отсюда
, отсюда
![]() , т. е.
, т. е.
3. Если
4. Свойства,
связанные с неравенствами. Если
Если
Доказательства этих свойств следуют из соответствующих свойств для сходящихся последовательностей и определения предела функции по Гейне.
5.6. Бесконечно малые и бесконечно большие функции
Функция
![]() называется
бесконечно малой функцией при
называется
бесконечно малой функцией при ![]() , если
, если
![]() при
при ![]() .
.
Пример 5.6.1.
![]() -- бесконечно малые
функции при
-- бесконечно малые
функции при ![]() .
.
Теорема 5.6.1.
а)
![]() -- бесконечно малая функция при
-- бесконечно малая функция при ![]() , если
, если
![]() и
и ![]() -- бесконечно малые функции при
-- бесконечно малые функции при ![]() ;
;
б)
![]() -- бесконечно малая функция при
-- бесконечно малая функция при ![]() , если
, если
![]() -- бесконечно малая функция при
-- бесконечно малая функция при ![]() , а функция
, а функция ![]() ограничена
в
ограничена
в ![]() ;
;
в) ![]() при
при
![]() , где
, где
![]() -- бесконечно малая функция при
-- бесконечно малая функция при ![]() .
.
Доказательство непосредственно следует из определения Гейне предела функции и соответствующих свойств бесконечно малых последовательностей.
Пример 5.6.2.
1)
![]() -- бесконечно малые функции при
-- бесконечно малые функции при ![]() ;
;
2)
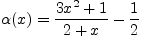 -- бесконечно
малая функция при
-- бесконечно
малая функция при ![]() .
.
Действительно, при ![]() рассмотрим
рассмотрим
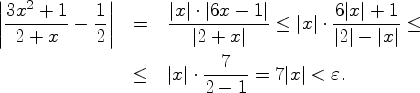
Функция ![]() называется
бесконечно большой функцией при
называется
бесконечно большой функцией при ![]() , если
, если
Пример 5.6.3.
![]() --
бесконечно большая функция при
--
бесконечно большая функция при ![]() .
.
Ясно, что если ![]() -- бесконечно большая функция при
-- бесконечно большая функция при ![]() , то
, то
![]() есть бесконечно малая функция при
есть бесконечно малая функция при ![]() и
наоборот.
и
наоборот.