Глава 4. Теоремы о полноте множества действительных чисел

4.1. Принцип вложенных отрезков

4.2. Точные границы множеств

4.3. Теорема Больцано-Вейерштрасса

4.4. Критерий Коши

Глава 4

Теоремы о полноте
множества действительных чисел

4.1. Принцип вложенных отрезков

Докажем несколько теорем, которые эквивалентны основному свойству множества действительных чисел $\mathbb{R}$ (свойству V).

Теорема 4.1.1 (Г.Кантора). Пусть задана система вложенных отрезков $\{\Delta_n\} = \{\left[a_n,b_n\right ] \}, \ n=1,2,\ldots\,,$ на ${\Bbb R}$, т. е. таких, что

$$\Delta_1\supseteq\Delta_2\supseteq\Delta_3\supseteq \ldots\supseteq\Delta_n\supseteq\ldots\,,$$

и длины отрезков $d_n=b_n-a_n\to0$ при $n\to\infty$. Тогда существует, и притом единственная, точка, одновременно принадлежащая всем отрезкам $\{\Delta_n\}$.

Доказательство. Возьмем любое $n\in{\Bbb N}$. Ясно, что для любого $k\in{\Bbb N}$ (из вложенности системы отрезков, см. рис. 4.1.1)

$$a_1\le a_2\le a_3\le\ldots\le a_k\le\ldots\le b_n\le\ldots\le b_2\le b_1\,.$$

Рис. 4.1.1

Рассмотрим последовательность левых концов отрезков системы $\left\{a_k\right\}$. Она монотонно возрастает и ограничена сверху, например, числом $b_n$. Тогда, по основной теореме 2.4.1, существует число (точка) $c\in{\Bbb R}$ такое, что $a_k\to c$ и для любого $k:\ a_k\le c\le b_n$. В частности, при $k=n:\ a_n\le c\le b_n$, что означает, что $c\in\Delta_n$. Так как $n$ было взято произвольным, то точка $c$ принадлежит всем отрезкам $\Delta_n,\ n=1,2,\ldots$.

Найденная точка единственная, так как, если существует $c_1\ne c$ и для любого $n:\ c_1,c\in \Delta_n$, то для любого $n$ выполняются неравенства $0<\vert c_1-c\vert\le b_n-a_n$, что противоречит тому, что $b_n-a_n\to0$ при $n\to\infty$.

Замечание 4.1.1. $a_n\nearrow c,\ b_n\searrow c$, т.е. последовательность $\{a_n\}$ левых концов отрезков $\Delta_n$, возрастая, стремится к точке $c$, а последовательность $\{b_n\}$ правых концов отрезков $\Delta_n$, убывая, стремится к $c$. Действительно,

$$\vert a_n-c\vert\le b_n-a_n\to0\quad \mbox{ и }\quad \vert b_n-c\vert\le b_n-a_n\to0.$$

Замечание 4.1.2. Во множестве рациональных чисел ${\Bbb Q}$ такого свойства, вообще говоря, нет. Например, пусть $c=\sqrt{2}\in{\Bbb R}$, а $\Delta_n=\left[c^{(n)}, c^{(n)}+\displaystyle{\frac{1}{10^n}}\right] \subset{\Bbb Q}$. Ясно, что эта последовательность отрезков удовлетворяет условиям теоремы Кантора, но общая единственная точка $c=\sqrt{2}$ -- иррациональное число, следовательно, во множестве рациональных чисел ${\Bbb Q}$ общих точек у рассматриваемой системы отрезков нет, т. е.

$$\bigcap_{n=1}^\infty\Delta_n=\varnothing\ \mbox{ в }\ {\Bbb Q}.$$

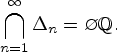
Замечание 4.1.3. То, что в теореме Кантора речь идет о системе отрезков (а, например, не интервалов), существенно. Достаточно рассмотреть систему интервалов 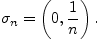${\Large\sigma}_n=\left(0,\displaystyle{\frac{1}{n}}\right).$ Ясно, что $\bigcap\limits_{n=1}^\infty{\Large\sigma}_n =\varnothing$ в ${\Bbb R}.$

4.2. Точные границы множеств

Рассмотрим произвольное множество $E$ действительных чисел. Если $E$ состоит из конечного числа элементов, то в $E$ имеется наименьшее число $m=\min E$ и наибольшее число $M=\max E$. Однако для бесконечных множеств наибольшие и наименьшие элементы не всегда существуют. Рассмотрим примеры:

$1)\ {\Bbb Z}=\left\{\ldots,-3,-2,-1,0,1,2,\ldots\right\}$;

$2)\ {\Bbb N}=\left\{1,2,\ldots\right\}$;

$3)\ \left[a,b\right]$;

$4)\ \left(a,b\right]$;

$5)\ \left(a,b\right)$.

Множество ${\Bbb Z}$ не имеет наименьшего и наибольшего элементов. Интервал $\left(a,b\right)$ тоже не имеет наименьшего и наибольшего элементов (хотя это множество ограничено), так как каково бы ни было число $c\in\left(a,b\right)$, всегда найдутся $c_1,\ c_2$ такие, что $a<c_1<c<c_2<b$. Множество ${\Bbb N}$ не имеет наибольшего элемента, но имеет наименьший элемент $x=1$. Очевидно, $\min[a,b]=a,\ \max[a,b]=b$, в $\left(a,b\right]$ нет наименьшего элемента.

Однако для бесконечных множеств, в которых нет наибольшего элемента, может существовать верхняя граница, которую нельзя уменьшить.

Множество $E\subset{\Bbb R}$ называется ограниченным сверху, если существует число $M\in{\Bbb R}$ такое, что для всех $x\in E:\ x\le M$. Число $M$ называется верхней границей (мажорантой) множества $E$.

Точной верхней границей множества $E\subset{\Bbb R}$ называется число $\mu\in{\Bbb R}$ такое, что

1) $\forall\ x\in E:\ x\le\mu$ (т.е. $\mu$ -- одна из верхних границ множества $E$);

2) $\forall\ \varepsilon >0\quad\exists\ x_\varepsilon \in E:\ \mu-\varepsilon <x_\varepsilon$ (т.е. границу $\mu$ множества $E$ нельзя уменьшить).

Точная верхняя граница множества $E$ обозначается
$\mu=\sup E$. Аналогично определяется точная нижняя граница множества, которую обозначают $\nu=\inf E$:

1) $\forall\ x\in E:\ x\ge\nu$ (т.е. $\nu$ -- одна из нижних границ множества $E$);

2) $\forall\ \varepsilon > 0\quad\exists\ x_\varepsilon \in E:\ x_\varepsilon <\nu+\varepsilon$ (т.е. границу $\nu$ множества $E$ нельзя увеличить).

Имеет место основная

Теорема 4.2.1. Если непустое множество действительных чисел ограничено сверху, то существует точная верхняя граница этого множества.

Доказательство (метод Больцано -- метод деления отрезка пополам). Пусть $x_0\in E\ne\varnothing$ и множество $E$ ограничено сверху числом $M$. Рассмотрим отрезок $\left[x_0,M\right]=\Delta_0$, заметим, что правее $\Delta_0$ нет точек из $E$. Разделим отрезок на два равных отрезка и обозначим $\Delta_1$ самый правый из них, содержащий хотя бы одну точку из $E$, т. е. правее $\Delta_1$ нет точек из $E$. Так же поступим с отрезком $\Delta_1$, получим отрезок $\Delta_2$, содержащий хотя бы одну точку из $E$, правее которого нет точек из $E$. Продолжив этот процесс по индукции, получим последовательность отрезков $\Delta_n=[a_n,b_n]$, длины которых $b_n-a_n=\displaystyle{\frac{M-x_0}{2^n}}\to0,\ \ n\to\infty$. При этом при любом $n\in{\Bbb N}$ правее $\Delta_n$ нет точек из $E$. На основании принципа вложенных отрезков (теорема 4.1.1) существует единственная точка $\mu\in{\Bbb R}$, лежащая во всех отрезках системы $\Delta_n$.

Докажем, что $\mu=\sup E$. В самом деле, по построению для всех $x\in E$ и для всех $n\in{\Bbb N}$ выполняется неравенство $x\le b_n$. Тогда, переходя к пределу в этом неравенстве при $n\to\infty$, получим (используя то, что $b_n\to \mu$) неравенство $x\le\mu$. Возьмем теперь любое $\varepsilon >0$. Тогда (так как и $a_n\to\mu$) существует номер $n\in{\Bbb N}$ такой, что $\mu-\varepsilon$ лежит левее отрезка $\Delta_n$. При этом в $\Delta_n$ лежит хотя бы одна точка $x_\varepsilon \in E$, т.е. выполняется неравенство $x_\varepsilon >\mu-\varepsilon$. Следовательно, $\mu=\sup E$.

Будем считать в дальнейшем, что если множество $E$ неограничено сверху, то $\sup E=+\infty$, если неограничено снизу, то $\inf E=-\infty$.

4.3. Теорема Больцано - Вейерштрасса

Пусть задана произвольная последовательность действительных чисел $\left\{x_n\right\}={x_1,x_2,\ldots}$ Последовательность $\left\{y_k\right\}:\ y_k=x_{n_k}$, где $n_1<n_2<\ldots<n_k<\ldots\,,$ называется подпоследовательностью последовательности $\left\{x_n\right\}$. Таких подпоследовательностей из заданной последовательности можно выделить бесконечно много.

Пример 4.3.1. Последовательность

$$\left\{y_k\right\}= \left\{\displaystyle{\frac{1}{2k}}\righ... ...splaystyle{\frac{1}{2},\frac{1}{4},\frac{1}{6}},\ldots\right\}$$

есть подпоследовательность последовательности

$$\left\{x_n\right\}=\left\{\displaystyle{\frac{1}{n}}\right\}... ...ac{1}{3},\frac{1}{4}, \frac{1}{5},\frac{1}{6}},\ldots\right\}.$$

Очевидно, имеет место

Теорема 4.3.1. Если последовательность $\left\{x_n\right\}$ сходится к некоторому пределу, то и любая ее подпоследовательность сходится к этому же пределу.

Пример 4.3.2. Последовательность $x_n=(-1)^n$ расходится, так как две ее подпоследовательности $y_{n_k}=x_{2k}=1$ и $z_{m_k}=x_{2k+1}=-1$ сходятся к разным числам.

Выделение подпоследовательностей у последовательности $\left\{x_n\right\}$, сходящихся к разным числам, есть один из методов доказательства ее расходимости.

Ответ на вопрос: "Во всякой ли последовательности можно выделить сходящуюся подпоследовательность'', дает следующая фундаментальная теорема.

Теорема 4.3.2 (Больцано - Вейерштрасса). Из всякой ограниченной последовательности $\left\{x_n\right\}\subset \mathbb{R}$ можно выделить подпоследовательность, сходящуюся к некоторому действительному числу.

Доказательство (метод Больцано). Так как последовательность $\left\{x_n\right\}$ ограничена, то существует число $M>0$ такое, что $\left\{x_n\right\}\subset\left[-M,M\right]=\Delta_0$. Разделим отрезок $\Delta_0$ на два равных отрезка и обозначим через $\Delta_1$ какой-нибудь из них, содержащий бесконечно много элементов из $\left\{x_n\right\}$, пусть $x_{n_1}\in\Delta_1$. Далее разделим отрезок $\Delta_1$ на два равных отрезка и обозначим через $\Delta_2$ какой-нибудь из них, содержащий бесконечно много элементов из $\left\{x_n\right\}$. Тогда найдется элемент $x_{n_2}\in\Delta_2$ и $n_2>n_1$. Процесс деления отрезка пополам, выбора одной из половин отрезка и элемента в ней продолжим по индукции. Итак, построена система вложенных отрезков $\Delta_1\supseteq\Delta_2\supseteq\Delta_3\supseteq \ldots\supseteq\Delta_n\supseteq\ldots$ и последовательность $\left\{x_{n_k}\right\}$ такая, что для любого $k$ выполняется $n_{k+1}>n_k$ и $x_{n_k}\in\Delta_k=\left[a_k,b_k\right]$. Тогда по теореме Кантора о вложенных отрезках существует единственная точка $c$, принадлежащая всем отрезкам, и $a_k\nearrow c,\ b_k\searrow c$. Переходя к пределу по $k\to\infty$ в неравенствах $a_k\le x_{n_k}\le b_k$, получим $x_{n_k}\to c$.

4.4. Критерий Коши

Из определения сходимости последовательности $\left\{x_n\right\}$ к точке $a$ вытекает, что для любого $\varepsilon >0$ интервалом длиной $2\varepsilon$ можно накрыть всю эту последовательность, исключая, может быть, конечное число ее элементов, если середину интервала поместить в точку $a$. Справедливо и обратное: если последовательность $\left\{x_n\right\}$ такова, что для любого $\varepsilon >0$ можно накрыть всю эту последовательность, исключая, может быть, конечное число ее элементов, поместив центр интервала в некоторую точку, то она сходится. Сформулируем это утверждение более точно. Последовательность $\left\{x_n\right\}$ назовем последовательностью Коши или фундаментальной, если

$$\forall\ \varepsilon > 0\quad \exists\ N(\varepsilon )\quad ... ...repsilon ):\quad \vert x_n-x_m\vert<\varepsilon \eqno(4.4.1)$$

(здесь центр интервала длиной $2\varepsilon$ помещен в точку $x_m,$ $m>N(\varepsilon )$, см. рис. 4.4.1).

Рис. 4.4.1

Теорема 4.4.1 (критерий Коши). Для того чтобы последовательность $\left\{x_n\right\}$ сходилась, необходимо и достаточно, чтобы она была фундаментальной.

Доказательство.
Необходимость (метод $\varepsilon/2$). Пусть $x_n\to~a$ при $n\to\infty$. Тогда для любого $\varepsilon >0$ существует номер $N(\varepsilon )$ такой, что для любых $n,m>N(\varepsilon )$ выполняются неравенства $\vert x_n-a\vert<\varepsilon /2,$ $\vert x_m-a\vert<\varepsilon /2$. Рассмотрим цепочку соотношений

$$\vert x_n-x_m\vert=\vert(x_n-a)+(a-x_m)\vert\le\vert x_n-a\vert+\vert x_m-a\vert<\varepsilon ,$$

что означает, что $\left\{x_n\right\}$ фундаментальна.

Достаточность. Докажем сначала ограниченность последовательности $\left\{x_n\right\}$. Возьмем $\varepsilon =1>0$, тогда, в силу фундаментальности $\left\{x_n\right\}$, найдется номер $N(\varepsilon )$ такой, что для всех $n,m>N(\varepsilon )$ выполняется $\vert x_n-x_m\vert<1$. Следовательно, $\vert x_n\vert-\vert x_m\vert\le\vert x_n-x_m\vert<1$, поэтому $\vert x_n\vert<1+\vert x_m\vert$. Итак, для всех $n>N(\varepsilon )$ при фиксированном $m>N(\varepsilon )$ выполняется $\vert x_n\vert<1+\vert x_m\vert$, что означает ограниченность последовательности $\left\{x_n\right\}$ (см. замечание 3.2.1). По теореме 4.3.2 из последовательности $\left\{x_n\right\}$ можно выделить подпоследовательность $\{x_{n_k}\}$, сходящуюся к некоторому числу $a$.

Докажем, что и вся последовательность $\left\{x_n\right\}$ сходится к числу $a$. Возьмем любое $\varepsilon >0$, тогда найдется номер $N$ (из фундаментальности $\left\{x_n\right\}$) такой, что для всех $n,m>N$ выполняется $\vert x_n-x_m\vert<\varepsilon /2$. Ввиду сходимости $x_{n_k}\to a$ при $k\to\infty$, по взятому $\varepsilon >0$ найдется номер $k_0$ такой, что $n_{k_0}>N$ и
$\vert x_{n_{k_0}}-a\vert<\varepsilon /2$. Тогда для нашего $n>N$

$$\vert x_n-a\vert=\vert x_n-x_m+x_m-a\vert=\left[x_m=x_{n_{k_0}}\right]\le$$

$$\le\vert x_n-x_m\vert+\vert x_{n_{k_0}}-a\vert<\varepsilon ,$$

что означает сходимость последовательности $\left\{x_n\right\}$ к числу $a$.

В главах 3-4 доказан ряд важнейших свойств множества действительных чисел ${\Bbb R}:$

1) существование предела у монотонной и ограниченной последовательности (теорема 3.1.2);

2) принцип вложенных отрезков (теорема 4.1.1);

3) существование точной верхней границы у произвольного ограниченного сверху множества (теорема 4.2.1);

4) существование сходящейся подпоследовательности у ограниченной последовательности (теорема 4.3.2);

5) критерий Коши сходимости числовой последовательности (теорема 4.4.1).

Хотя перечисленные свойства действительных чисел сформулированы в различных терминах, на самом деле у них имеется глубокая внутренняя связь. Можно показать, что все эти утверждения эквивалентны. Мы показали лишь, что из свойства 1 следует свойство 2, из свойства 2 следуют свойства 3 и 4, из свойства 4 -- свойство 5. Свойства 1-5 называются еще свойствами непрерывности, или полноты, множества действительных чисел ${\Bbb R}$.