Элементарное представление о действительных числах дается в курсе средней школы. Однако этого представления недостаточно для строгого и последовательного построения понятия предела и бесконечно малой величины.
2.1. Рациональные числа и их свойств
Основными, неопределяемыми понятиями
в теории действительных чисел являются натуральные числа
Из потребностей счета множество натуральных чисел было расширено с сохранением
арифметических операций до множества целых чисел
Если считать, что ![]() , то
, то
![]() . В множестве
. В множестве ![]() всегда выполнимы операции "
всегда выполнимы операции "![]() ", "
", "![]() " и "
" и "![]() ", а операция "
", а операция "![]() "
выполнима не всегда.
"
выполнима не всегда.
Множество целых чисел может быть расширено с сохранением операций
до множества рациональных чисел
Отношения порядка, равенства и арифметические операции в ![]() вводятся известным образом. Напомним основные определения, касающиеся рациональных чисел:
вводятся известным образом. Напомним основные определения, касающиеся рациональных чисел:
Множество всех рациональных чисел относительно так введенных операций сложения и умножения и отношения порядка обладает следующими фундаментальными свойствами.
Пусть ![]() -- любые числа из
-- любые числа из ![]() .
.
![]() Имеет место одно и только одно соотношение
для двух чисел:
Имеет место одно и только одно соотношение
для двух чисел:
Эти свойства можно доказать, исходя из определения рациональных чисел и операций над ними.
Числовой осью называют прямую, на которой выбраны точка ![]() масштабный
отрезок
масштабный
отрезок ![]() и положительное направление.
и положительное направление.
Каждому рациональному числу ![]() можно поставить в соответствие единственную точку
можно поставить в соответствие единственную точку ![]() на
числовой оси (см. рис. 2.2.1). Для этого нужно разделить масштабный отрезок
на
числовой оси (см. рис. 2.2.1). Для этого нужно разделить масштабный отрезок ![]() на
на ![]() равных частей и
равных частей и ![]() -ю долю отложить
-ю долю отложить ![]() раз от точки
раз от точки ![]() в нужном направлении.
в нужном направлении.
Пример 2.2.1. Сторона и диагональ квадрата несоизмеримы. Действительно, примем
длину стороны квадрата за единицу и допустим, что его диагональ соизмерима со стороной.
Тогда длина диагонали выражается некоторой дробью ![]() .
Можно считать, что эта дробь несократима.
По теореме Пифагора
.
Можно считать, что эта дробь несократима.
По теореме Пифагора
Следовательно, существуют несоизмеримые отрезки, и поэтому не всем точкам числовой оси можно поставить в соответствие рациональные числа.
Этот геометрический факт существования несоизмеримых отрезков может быть выражен в виде
алгебраической задачи: уравнение ![]() не имеет решения в области рациональных чисел.
не имеет решения в области рациональных чисел.
Необходимо расширение множества рациональных чисел с сохранением операций и всех свойств I-IV, перечисленных выше, так, чтобы существовало взаимно-однозначное соответствие между точками числовой оси и этими новыми числами.
2.3. Бесконечные десятичные дроби.
Действительные числа
Из изложенного выше необходимы новые объекты, среди которых найдутся такие, которые
соответствуют рациональным числам ![]() , и арифметические операции в этих новых
числах согласуются с соответствующими операциями в
, и арифметические операции в этих новых
числах согласуются с соответствующими операциями в ![]() . Такими объектами
являются бесконечные десятичные дроби
. Такими объектами
являются бесконечные десятичные дроби
Множество всех таких бесконечных десятичных дробей обозначим ![]() (для удобства
исключим из рассмотрения бесконечные десятичные дроби с 9 в периоде).
(для удобства
исключим из рассмотрения бесконечные десятичные дроби с 9 в периоде).
Важно отметить, что каждую рациональную дробь ![]() , используя алгоритм деления, можно
записать в виде бесконечной периодической дроби. Действительно, остаток от деления
, используя алгоритм деления, можно
записать в виде бесконечной периодической дроби. Действительно, остаток от деления ![]() на
на
![]() может быть одним из чисел
может быть одним из чисел
![]() , и при неограниченном процессе
деления остатков на
, и при неограниченном процессе
деления остатков на ![]() неминуемо какой-то из остатков повторится, а значит, повторится
бесконечное число раз.
неминуемо какой-то из остатков повторится, а значит, повторится
бесконечное число раз.
Задача 2.3.1. Проверьте делением столбиком, что
Таким образом, все рациональные числа содержатся среди бесконечных десятичных дробей как периодические бесконечные десятичные дроби.
Действительными числами называют бесконечные десятичные дроби. В случае периодичности дроби такое действительное число называют рациональным, в противном случае -- иррациональным.
Пример 2.3.1. Число
![]() как непериодическая бесконечная
десятичная дробь есть число иррациональное.
как непериодическая бесконечная
десятичная дробь есть число иррациональное.
Сравнительно просто определять в ![]() отношение равенства и порядка
("больше"). Рассмотрим два действительных числа
отношение равенства и порядка
("больше"). Рассмотрим два действительных числа
Пусть ![]() одного знака "
одного знака "![]() ''. Число
''. Число ![]() больше числа
больше числа ![]()
![]() ,
если либо
,
если либо
![]() , либо существует номер
, либо существует номер ![]() такой, что
такой, что
![]() для
для
![]() и
и
![]() .
.
Пример 2.3.2.
![]() , здесь
, здесь ![]() .
.
2.4. Стабилизирующиеся последовательности
Если каждому натуральному
![]() поставлено в
соответствие число
поставлено в
соответствие число
![]() , совокупность
, совокупность
Пример 2.4.1. Приведем несколько примеров числовых последовательностей:
a) 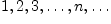
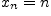 ;
;
б) 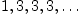
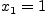 и
и 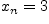 , если
, если 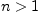 ;
;
в) 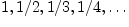
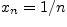 ;
;
г) 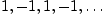
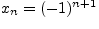 .
.
Последовательность ![]() называется возрастающей (будем обозначать
называется возрастающей (будем обозначать
![]() ), если
), если
![]() ;
ограниченной
сверху, если
;
ограниченной
сверху, если
![]() .
.
Аналогично вводятся понятия убывающей и ограниченной снизу последовательностей. Последовательности, ограниченные снизу и сверху, называются ограниченными.
Последовательности а) и б) из примера 2.4.1 монотонно возрастают, последовательность в) монотонно
убывает, последовательность г) не монотонна. Последовательности а), б), в), г)
ограничены снизу, а последовательности б), в), г) ограничены сверху. Последовательность
а) не ограничена сверху, так как для нее выполняется условие
![]() (отрицание ограниченности
(отрицание ограниченности
![]() сверху).
сверху).
Действительно, для любого числа ![]() за
номер
за
номер ![]() можно взять непосредственно следующее за
можно взять непосредственно следующее за
![]() натуральное
число, тогда
натуральное
число, тогда
![]() .
.
Последовательность целых чисел ![]() называется
стабилизирующейся к целому числу
называется
стабилизирующейся к целому числу ![]() при
при ![]() , стремящемся к
, стремящемся к ![]() , если найдется
номер
, если найдется
номер ![]() такой, что для всех
такой, что для всех
![]() .
.
Последовательность б) в примере 2.4.1 стабилизируется к целому числу 3. Из свойств целых
чисел ясно, что если последовательность ![]() монотонно возрастает и ограничена сверху
числом
монотонно возрастает и ограничена сверху
числом ![]() , то
, то ![]() стабилизируется к некоторому числу, не превосходящему
стабилизируется к некоторому числу, не превосходящему ![]() .
.
Рассмотрим теперь последовательность неотрицательных бесконечных десятичных дробей
![]() :
:
![]()
![]()
![]()
Говорят, что последовательность бесконечных десятичных дробей
![]() стабилизируется при
стабилизируется при ![]() к бесконечной десятичной дроби
к бесконечной десятичной дроби
![]() (обозначается
(обозначается
![]() ), если для любого
номера
), если для любого
номера
![]() столбец
столбец
![]() таблицы (2.4.2) с номером
таблицы (2.4.2) с номером ![]() стабилизируется к числу
стабилизируется к числу ![]() при
при ![]() .
Это фактически означает, что последовательность
.
Это фактически означает, что последовательность ![]() поразрядно
сходится к числу
поразрядно
сходится к числу ![]() .
.
Пример 2.4.2. Пусть ![]() -- неотрицательное действительное число,
-- неотрицательное действительное число,
![]() Тогда рациональную десятичную дробь
Тогда рациональную десятичную дробь
![]() называют
называют ![]() -м приближением числа
-м приближением числа
![]() по недостатку. Очевидно, что
по недостатку. Очевидно, что
![]() при
при ![]() и
и
![]() .
.
Сформулируем основное свойство действительных чисел, которое,
вообще говоря, не выполняется в ![]() .
.
Теорема 2.4.1 (Свойство V). Если последовательность неотрицательных
бесконечных десятичных дробей ![]() возрастает и ограничена сверху числом
возрастает и ограничена сверху числом ![]() , то
существует число
, то
существует число ![]() такое, что
такое, что
![]() ,
,
![]() .
.
Доказательство. 1) Рассмотрим таблицу (2.4.2). В ней нулевой столбец целых чисел
является возрастающей последовательностью, иначе сама последовательность ![]() не
будет возрастающей, и ограничен сверху числом
не
будет возрастающей, и ограничен сверху числом ![]() . Следовательно, существует целое
. Следовательно, существует целое
![]() такое, что
такое, что ![]() стабилизируется к
стабилизируется к ![]() , т.е.
, т.е.
![]() , начиная с некоторого номера
, начиная с некоторого номера ![]() . Столбец
. Столбец ![]() , начиная с
номера
, начиная с
номера ![]() , является возрастающей последовательностью и, будучи ограниченным сверху
числом
, является возрастающей последовательностью и, будучи ограниченным сверху
числом ![]() , стабилизируется к некоторому числу
, стабилизируется к некоторому числу ![]() , начиная с номера
, начиная с номера ![]() .
.
И так далее -- все столбцы таблицы (2.4.2) стабилизируются. Из определения
получаем, что ![]() стабилизируется к некоторому числу
стабилизируется к некоторому числу
![]() .
.
2) По построению числа ![]() ,
, ![]() для всех
для всех ![]() . Докажем, что
. Докажем, что ![]() . Пусть, напротив,
. Пусть, напротив, ![]() , тогда по
определению "больше'' найдется номер
, тогда по
определению "больше'' найдется номер
![]() такой, что
такой, что ![]() -е приближение по
недостатку числа
-е приближение по
недостатку числа ![]()
Если теперь взять номер ![]() (построенный в пункте 1), получим
(построенный в пункте 1), получим
2.5. Арифметические операции в ![]()
Рассмотрим положительные действительные числа
Остальные арифметические операции определяются в ![]() аналогично.
аналогично.
Можно проверить, что выполняются свойства I(1-3)
, II(1-5), III(1-6), IV и, кроме того, выполняется еще одно свойство V
(теорема 2.4.1),
которого не было в ![]() .
.
Можно доказать, что арифметические операции с рациональными
числами, как дробями и как периодическими десятичными дробями, описанными выше, приводят
к одному результату. Таким образом, множество рациональных чисел ![]() расширено
до множества
расширено
до множества ![]() действительных чисел с сохранением арифметических операций.
действительных чисел с сохранением арифметических операций.
2.6. Модуль действительного числа. Основные неравенства, окрестности
Напомним определение модуля числа ![]() :
:
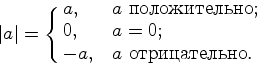
Геометрически модуль числа ![]() означает расстояние от числа
означает расстояние от числа ![]() до нуля. Соответственно,
до нуля. Соответственно,
![]() означает расстояние от точки
означает расстояние от точки ![]() до точки
до точки ![]() на числовой прямой (см. рис.
2.6.1).
на числовой прямой (см. рис.
2.6.1).
3)
![]() .
.
Доказательство. Докажем свойство 2. Возможны несколько различных случаев
расположения чисел ![]() и
и ![]() относительно нуля:
относительно нуля:
1)
![]() , тогда
, тогда
![]() ;
;
2) ![]() , тогда
, тогда
![]() ;
;
3) ![]() и пусть
и пусть ![]() . Тогда
. Тогда
![]() и
и
![]() .
.
Остальные случаи разбираются аналогично.
Наконец, отметим, что неравенство
![]() равносильно двойному неравенству
равносильно двойному неравенству
![]() , и неравенство
, и неравенство
![]() можно записать в
эквивалентном виде
можно записать в
эквивалентном виде
![]() , или
, или
![]() .
.
Окрестностью точки ![]() радиуса
радиуса ![]() называется множество всех точек
(см. рис. 2.6.2), находящихся от точки
называется множество всех точек
(см. рис. 2.6.2), находящихся от точки ![]() на расстоянии строго меньше
на расстоянии строго меньше ![]() , и
обозначается это множество через
, и
обозначается это множество через ![]() .
Таким образом, по определению
.
Таким образом, по определению