Свойства отношения порядка:
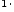 Имеет место одно и только одно соотношение
для двух чисел:
Имеет место одно и только одно соотношение
для двух чисел:
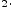 Транзитивность отношения "больше''
Транзитивность отношения "больше''
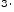 Свойство плотности множества
Свойство плотности множества 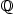
Свойства операции сложения:
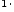
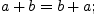
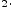
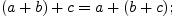
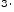
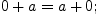
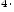
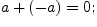
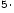
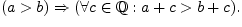
Свойства операции умножения:
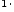
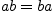 ;
;
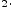
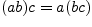 ;
;
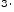
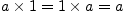 ;
;
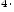
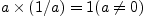 ;
;
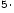
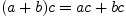 ;
;
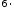
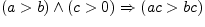 .
.
Свойство Архимеда:
Пусть даны две функции 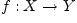 и
и 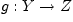 . Функция
. Функция 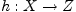 ,
определяемая равенством
,
определяемая равенством
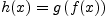 , называется
сложной функцией (или
суперпозицией функций) от
, называется
сложной функцией (или
суперпозицией функций) от 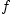 и
и 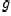 .
.
Последовательность целых чисел 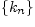 называется
стабилизирующейся
к целому числу
называется
стабилизирующейся
к целому числу 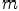 при
при 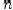 , стремящемся к
, стремящемся к 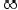 , если найдется
номер
, если найдется
номер 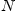 такой, что для всех
такой, что для всех
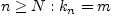 .
.
Верхняя сумма Дарбу:
Нижняя сумма Дарбу:
Последовательность 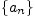 называется
сходящейся,
если существует число
называется
сходящейся,
если существует число 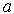 , к которому она сходится, т.е.
, к которому она сходится, т.е.

