3.1. Сходящиеся и стабилизирующиеся
последовательности
Число ![]() называется пределом последовательности
называется пределом последовательности ![]() (по Коши)
(по Коши)
Последовательность ![]() называется сходящейся,
если существует число
называется сходящейся,
если существует число ![]() , к которому она сходится, т.е.
, к которому она сходится, т.е.
Пример 3.1.1. Докажем, что
![$N(\varepsilon )=\left[\displaystyle{\frac{1}{\varepsilon }}\right]+1$](../img/img279.gif) . Здесь
. Здесь
И теперь
![$\forall\ n>N(\varepsilon )=\left[\displaystyle{\frac{1}{\varepsilon }}\right]+1$](../img/img282.gif) выполняются
соотношения
выполняются
соотношения
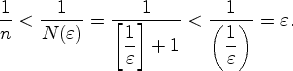
Пример 3.1.2. Докажем, что
![$N(\varepsilon )=\left[\displaystyle{\frac{1}{\varepsilon }}\right]+1$](../img/img279.gif) .
.
Пример 3.1.3. Докажем, что
![\begin{eqnarray*}
\left\vert\frac{3n+5}{5n-3}-\frac{3}{5}\right\vert &=&\frac{34...
...3$}\right] \le \\ &\le&\frac{8}{5n-n}=\frac{2}{n}<\varepsilon .
\end{eqnarray*}](../img/img287.gif)
![$N(\varepsilon )=\left[\displaystyle{\frac{2}{\varepsilon }}\right]+3$](../img/img288.gif) .
.
Теорема 3.1.1. Если
![]() , то
, то ![]() .
.
Доказательство. Возьмем любое
![]() . Как и в примере 3.1.2, найдется
. Как и в примере 3.1.2, найдется
![]() . Так как
. Так как
![]() , то в таблице (2.4.2)
столбцы, начиная с нулевого по
, то в таблице (2.4.2)
столбцы, начиная с нулевого по ![]() -й, стабилизируются, начиная с номера
-й, стабилизируются, начиная с номера ![]() .
Следовательно, для любого
.
Следовательно, для любого ![]()
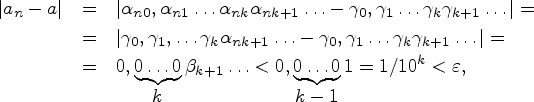
Свойство V множества действительных чисел ![]() может теперь быть
сформулировано следующим образом.
может теперь быть
сформулировано следующим образом.
Теорема 3.1.2 (Свойство V).
Если последовательность ![]() монотонно возрастает и
ограничена сверху числом
монотонно возрастает и
ограничена сверху числом
![]() , то существует число
, то существует число
![]() такое, что
такое, что
![]()
![]() при
при ![]() ;
;
![]() для любого
для любого
![]() .
.
3.2. Свойства сходящихся последовательностей
Иногда удобно записывать определение сходимости последовательности
![]() в следующих эквивалентных первоначальному видах:
в следующих эквивалентных первоначальному видах:
![]()
![]()
![]()
вне окрестности
![]() лежит конечное число элементов последовательности
лежит конечное число элементов последовательности ![]() .
.
Свойство 3.2.1. Если последовательность ![]() сходится,
то ее предел единственный.
сходится,
то ее предел единственный.
Доказательство (от противного). Пусть
Последовательность ![]() называется
ограниченной, если
называется
ограниченной, если
![]() . Это означает, что
. Это означает, что
![]() или что множество
или что множество ![]() можно накрыть отрезком
можно накрыть отрезком ![]() .
.
Замечание 3.2.1.
Ясно, что последовательность ![]() будет ограниченной,
если ее можно накрыть отрезком
будет ограниченной,
если ее можно накрыть отрезком ![]() , начиная с некоторого номера
, начиная с некоторого номера ![]() . (Вне отрезка
. (Вне отрезка
![]() может лежать лишь конечное число элементов последовательности
может лежать лишь конечное число элементов последовательности ![]() ,
следовательно, и всю последовательность можно накрыть некоторым отрезком
,
следовательно, и всю последовательность можно накрыть некоторым отрезком ![]() ,
где
,
где ![]() ).
).
Свойство 3.2.2. Если последовательность сходится, то она ограничена.
Доказательство. Пусть ![]() и
и
![]() . Тогда, по определению сходимости,
существует номер
. Тогда, по определению сходимости,
существует номер ![]() такой, что для всех
такой, что для всех
![]() . Следовательно,
. Следовательно,
![]() , и поэтому
, и поэтому
![]() . Итак, по
замечанию 3.2.1, последовательность
. Итак, по
замечанию 3.2.1, последовательность ![]() ограничена.
ограничена.
Свойство 3.2.3. Если последовательность ![]() сходится к числу
сходится к числу ![]() , то вся последовательность
, то вся последовательность ![]() лежит вне окрестности нуля
лежит вне окрестности нуля
![]() ,
начиная с некоторого номера.
,
начиная с некоторого номера.
Для доказательства достаточно взять
![]() . Тогда, по определению
предела, найдется
. Тогда, по определению
предела, найдется
![]() , что для всех
, что для всех
![]() ,
следовательно,
,
следовательно,
![]() .
.
Свойство 3.2.4. Если ![]() для всех
для всех ![]() и
и
Доказательство. Пусть, напротив,
Свойство 3.2.5. Если
![]() для всех
для всех ![]() и
и
Доказательство. Проверим, что выполняется определение
сходимости последовательности ![]() к числу
к числу ![]() . Возьмем любое
. Возьмем любое
![]() , тогда из условия
, тогда из условия
![]() следует, что
следует, что
Пример 3.2.1.
Докажем, что
![]() .
.
Действительно, для любого
![]() , используя результат задачи 1.4.1, получим
, используя результат задачи 1.4.1, получим
Пример 3.2.2.
Докажем, что
![]() , где
, где
![]() .
.
Рассуждая так же, как в задаче 3.2.1, имеем
3.3. Бесконечно малые и бесконечно
большие
последовательности
Удобным инструментом при изучении предельных переходов является понятие бесконечно малой последовательности.
Последовательность ![]() называется
бесконечно малой, если
называется
бесконечно малой, если ![]() при
при ![]() . Развернутое определение:
. Развернутое определение:
Свойство 3.3.1. Сумма и разность
бесконечно малых последовательностей ![]() и
и ![]() есть бесконечно малая
последовательность.
есть бесконечно малая
последовательность.
Доказательство. Возьмем произвольное
![]() .
Для него
.
Для него
Свойство 3.3.2.
Произведение
![]() бесконечно малой последовательности
бесконечно малой последовательности ![]() на ограниченную
последовательность
на ограниченную
последовательность ![]() есть бесконечно малая последовательность.
есть бесконечно малая последовательность.
Доказательство. Из ограниченности ![]() следует существование числа
следует существование числа ![]() такого, что для всех
такого, что для всех
![]() . Следовательно, при любом положительном
. Следовательно, при любом положительном
![]() для положительного
для положительного
![]() существует
номер
существует
номер
![]() такой, что для всех
такой, что для всех
![]() . Поэтому для этих
. Поэтому для этих
![]() имеем
имеем
![]() .
Следовательно, по определению
Коши,
.
Следовательно, по определению
Коши,
![]() при
при ![]() .
.
Свойство 3.3.3.
Для того чтобы
последовательность ![]() была сходящейся, необходимо и достаточно, чтобы существовали
число
была сходящейся, необходимо и достаточно, чтобы существовали
число
![]() и бесконечно малая последовательность
и бесконечно малая последовательность ![]() такие, что
для всех
такие, что
для всех
![]() выполнялось равенство
выполнялось равенство
![]() .
.
Доказательство.
Необходимость.
Пусть ![]() при
при ![]() . Рассмотрим
. Рассмотрим
![]() , тогда из определения
сходимости
, тогда из определения
сходимости ![]() следует, что
следует, что ![]() при
при ![]() .
.
Достаточность. Если
![]() , то из того, что
, то из того, что ![]() -- бесконечно
малая последовательность и
-- бесконечно
малая последовательность и
![]() следует, что
следует, что ![]() при
при ![]() .
.
Последовательность ![]() называется
бесконечно большой, если
называется
бесконечно большой, если
Пример 3.3.1.
 -- бесконечно малые последовательности (см. примеры 3.1.1 и 3.1.2),
-- бесконечно малые последовательности (см. примеры 3.1.1 и 3.1.2), ![]() -- бесконечно большая
последовательность. Действительно, возьмем любое
-- бесконечно большая
последовательность. Действительно, возьмем любое ![]() , рассмотрим неравенство
, рассмотрим неравенство
![]() , тогда
, тогда ![]() и для любого
и для любого ![]()
Пример 3.3.2.
 при
при ![]() , если
, если ![]() .
Действительно,
.
Действительно,
Бесконечно малые и бесконечно большие последовательности тесно связаны между собой.
Теорема 3.3.1. Последовательность
![]() является бесконечно малой
последовательностью тогда и только тогда, когда последовательность
является бесконечно малой
последовательностью тогда и только тогда, когда последовательность
![]() является бесконечно большой.
является бесконечно большой.
Доказательство следует
из того факта, что неравенство
![]() равносильно
неравенству
равносильно
неравенству
![]() , и
определений бесконечно малых и бесконечно больших последовательностей.
, и
определений бесконечно малых и бесконечно больших последовательностей.
3.4. Свойства пределов, связанные
с арифметическими операциями
Свойство 3.4.1. Если последовательности ![]() и
и ![]() сходятся, то сходится последовательность
сходятся, то сходится последовательность
![]() и
и
![]()
Свойство 3.4.2. Если последовательности ![]() и
и ![]() сходятся, то сходится последовательность
сходятся, то сходится последовательность ![]() и
и
Доказательство. Пусть
![]() .
.
Тогда
![]() и
и
![]() при
при ![]() . Поэтому
. Поэтому
Свойство 3.4.3. Если последовательности ![]() и
и ![]() сходятся к
сходятся к ![]() и
и ![]() соответственно, то последовательность
соответственно, то последовательность
![]() сходится к
сходится к
![]()
Доказательство. Так как ![]() (пусть для определенности
(пусть для определенности
![]() ), то по свойству 3.2.3, начиная с некоторого номера
), то по свойству 3.2.3, начиная с некоторого номера
![]() .
Поэтому определена
последовательность
.
Поэтому определена
последовательность
![]()
![]() и
и
![]() Рассмотрим для номеров
Рассмотрим для номеров ![]() цепочку равенств
цепочку равенств
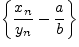 -- бесконечно
малая последовательность, следовательно, по свойству 3.3.3, последовательность
-- бесконечно
малая последовательность, следовательно, по свойству 3.3.3, последовательность
Пример 3.4.1.
Найдем
Пример 3.4.2. Найдем
Пример 3.4.3. Найдем
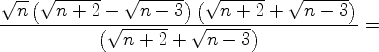
Рассмотрим последовательность
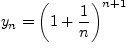 . Докажем, что эта
последовательность убывает и, так как
. Докажем, что эта
последовательность убывает и, так как ![]() ограничена снизу, например, числом
ограничена снизу, например, числом ![]() ,
то она сходится к некоторому числу. Действительно, рассмотрим отношение соседних членов
последовательности
,
то она сходится к некоторому числу. Действительно, рассмотрим отношение соседних членов
последовательности ![]() :
:
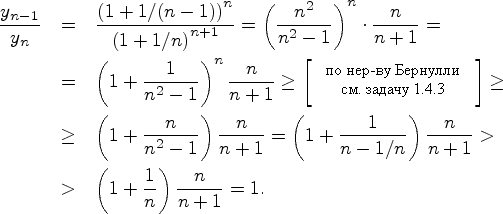
Следовательно, последовательность
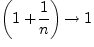 , то
, то
Замечание. Мы "раскрыли" простейшую неопределенность вида
![]() .
.
Задача 3.5.1. Доказать, что
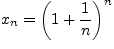 возрастает и ограничена сверху.
возрастает и ограничена сверху.