all_book

Глава 1. Элементы теории множеств и математической логики: 1.1. Алгебра высказываний; 1.2. Предикаты и кванторы; 1.3. Метод математической индукции; 1.4. Элементы теории множеств

Глава 1

Элементы теории множеств
и математической логики

Любая современная математическая теория начинается с соглашений об основных понятиях этой теории, которые не определяются через другие понятия, и основных положений, которые принимаются без доказательств, как данные практической деятельности человека, как всем известное. А далее построение ведется по законам логики и внутренним потребностям самой этой математической теории.

В математической логике как математической теории основными неопределяемыми понятиями являются понятия суждение, истина, ложь. Суждение не может быть одновременно истинным и ложным. Например, все предложения, которые произносит человек, являются суждениями.

Высказыванием называется суждение, которому можно приписать истину или ложь. Например, суждение "Снег белый" есть истинное высказывание; суждение "Число 6 делится на 4" -- ложное высказывание; суждение "Который час?" не является высказыванием.

Из высказываний $A, B,\,\ldots$ можно построить новые высказывания с помощью логических операций $\left(\bigwedge, \bigvee, \overline{\phantom{aa}}, \Rightarrow, \Leftrightarrow \right)$ . Приведем определения этих операций.

Отрицанием высказывания называется такое высказывание, обозначаемое $\overline A$ (читается: "не "), которое является истинным, если ложно, и ложным, если истинно. Эту ситуацию можно изобразить с помощью таблицы истинности:

	$\overline A$
и	л
л	и

Конъюнкцией высказываний и называется высказывание, обозначаемое $A\bigwedge B$ (читается: " и ''), которое истинно, если истинны оба высказывания и , и ложно в остальных случаях (см. таблицу):

		$A\bigwedge B$
и	и	и
и	л	л
л	и	л
л	л	л

Дизъюнкцией высказываний и называется высказывание, обозначаемое $A\bigvee B$ (читается: " или "), которое ложно, если ложны оба эти высказывания и , и истинно в остальных случаях (см. таблицу):

		$A\bigvee B$
и	и	и
и	л	и
л	и	и
л	л	л

Импликацией высказываний и называется высказывание, обозначаемое $A\Rightarrow B$ (читается: "из следует " или "если , то ''), которое ложно, если истинно, а ложно, и истинно в остальных случаях (см. таблицу):

		$A\Rightarrow B$
и	и	и
и	л	л
л	и	и
л	л	и

Всем теоремам в математике, как высказываниям, можно придать вид импликации двух высказываний: $T\equiv(A\Rightarrow B$ ). Высказывание называют условием теоремы , а высказывание -- заключением теоремы . Или высказывание называют необходимым условием для высказывания , а высказывание -- достаточным условием для высказывания в теореме $T\equiv(A\Rightarrow B$ ).

Пример 1.1.1. $T\equiv$ "все натуральные числа, делящиеся на 4, делятся на 2" или, иначе, $T\equiv$ "если число делится на 4, то число делится на 2". Здесь приведена импликация, которая истинна, и высказывание $B\equiv$ "число делится на 2" есть необходимое условие для высказывания $A\equiv$ "число делится на 4", а высказывание является достаточным условием для высказывания в этой теореме .

Эквиваленцией высказываний и называется высказывание, обозначаемое $A\Leftrightarrow B$ (читается: " эквивалентно ''), которое истинно, когда высказывания и истинны или ложны одновременно (т.е. их таблицы истинности совпадают).

Итак, при помощи логических операций построено множество высказываний, которое называют алгеброй высказываний.

Основные формулы алгебры высказываний:
1. ${\overline{\left(\overline A \right)}}\Leftrightarrow A$ ;
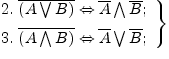$\left.\begin{array}{ll} \hspace{-2mm} 2. \hspace{1mm} {\overline{\left(A\bigv... ...ht)}}\Leftrightarrow{{\overline A} \bigvee{\overline B}}; \end{array}\right\}$ законы де Моргана
4. ${\left(A\Rightarrow B\right)}\Leftrightarrow{{\overline A} \bigvee B};$
5. ${\overline{\left(A\Rightarrow B\right)}}\Leftrightarrow{ A \bigwedge{\overline B}}.$
Эти формулы могут быть доказаны сравнением соответствующих таблиц истинности.

Из двух высказываний и можно составить четыре импликации, которые носят названия:

$A\Rightarrow B$ -- прямая теорема;

$B\Rightarrow A$ -- обратная теорема;

${\overline A} \Rightarrow {\overline B}$ -- противоположная теорема;

${\overline B} \Rightarrow {\overline A}$ -- теорема, противоположная к обратной.

Из основных формул алгебры высказываний следует, что:

${\left(A\Rightarrow B\right)}\Leftrightarrow {\left({\overline B}\Rightarrow {\overline A}\right)}$ ;

${\left(B\Rightarrow A\right)}\Leftrightarrow {\left({\overline A}\Rightarrow {\overline B}\right)}$ .

Следует отметить, что из истинности прямой теоремы еще не следует истинность обратной к ней теоремы, как это видно из примера 1.1.1.

Доказать истинность теоремы $\left(A\Rightarrow B\right)$ можно, доказав истинность теоремы $\left({\overline B}\Rightarrow {\overline A}\right)$ , так как эти теоремы эквивалентны. На этом основано доказательство от противного теоремы $\left(A\Rightarrow B\right)$ , а именно: имея истинность , предполагая истинность $\overline B$ и доказав, что из $\overline B$ следует $\overline A$ , мы получаем противоречие ( и $\overline A$ одновременно истинны), что не может быть, значит, $\overline B$ ложно, тогда истинно и, значит, импликция $A\Rightarrow B$ истинна.

1.2. Предикаты и кванторы

Суждение, зависящее от переменной величины, которое при подстановке значений переменного становится высказыванием, называют предикатом.

Пример 1.2.1. $A(x)\equiv$ {река впадает в Каспийское море} есть предикат, зависящий от одного переменного , здесь -- одноместный предикат.

$B(x,y)=\{x^2+y^2=1\}$ -- двуместный предикат.

Как и из высказываний, при помощи логических операций $\left(\bigwedge, \bigvee, \overline{\phantom{aa}}, \Rightarrow, \Leftrightarrow \right)$ можно строить новые предикаты, и мы получим алгебру предикатов.

С помощью кванторов $\forall\$ (всеобщности) и $\exists\$ (существования) можно строить из предикатов новые предикаты и высказывания.

1. $\left(\forall\ x\right):\ A(x)$ (читается, а часто и пишется: "для всех выполняется ''). Это будет высказывание, которое истинно, если предикат истинен для всех из его области определения, и ложным -- в противном случае.

Пример 1.2.2. $\left(\forall\ x\right)$ : {река впадает в Каспийское море} есть ложное высказывание; $\left(\forall\ x\right):\ \{x^2\geq 0\}$ -- истинное высказывание.

2. $\left(\exists\ x\right): A(x)$ (читается и пишется: "существует , для которого выполняется ''). Это будет высказывание, которое истинно, если предикат истинен на каком-то конкретном из его области определения.

Например, $\left(\exists\ x\right)$ : {река впадает в Каспийское море} -- истинное высказывание, так как, например, река Урал впадает в Каспийское море; $\left(\exists\ x\right):\{ {x^2+1}<0\}$ -- ложное высказывание.

Построим отрицание высказывания $\left(\forall\ x\right):\ A(x)$ .

Если данное утверждение не имеет места, то суждение имеет место не для всех , т.е. существует элемент , для которого не имеет места:

$\begin{displaymath} \overline{\left(\forall\ x\right):\ A(x)}\Leftrightarrow \left(\exists\ x\right):\overline{A(x)}. \end{displaymath}$

Совершенно аналогично

$\begin{displaymath} \overline{\left(\exists\ x\right):\ A(x)}\Leftrightarrow \left(\forall\ x\right):\ \overline{A(x)}. \end{displaymath}$

Таким образом, чтобы построить отрицание логической формулы, содержащей кванторы $\forall\$ и $\exists\,$ , необходимо квантор $\forall\$ заменить на квантор $\exists\,$ , а квантор $\exists\$ заменить на квантор $\forall\,$ и отрицание (черту сверху) отнести на предикат.

Пример 1.2.3.

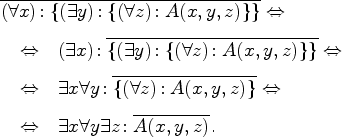
$\begin{eqnarray*} \lefteqn{ {\overline{\left(\forall\ x\right)\!: \left\{\left(\... ...w & {\exists\ x\ \forall\ y\ \exists\ z}\!: \overline{A(x,y,z)}. \end{eqnarray*}$

Заметим, что скобки и двоеточия можно частично или вовсе опускать при записи такого рода логических формул, если не возникает разночтений.

1.3. Метод математической индукции

Некоторые высказывания могут зависеть от натурального переменного. Например, $\forall\ n:\ 1+2+\ldots+n=n(n+1)/2$ . Для доказательства истинности такого рода высказываний может использоваться метод, основанный на свойствах натурального ряда чисел, называемый методом математической индукции.

Высказывание $\forall\ n:\ A(n)$ истинно, если выполняются следующие условия:

1. (База индукции.) Высказывание истинно для .

2. (Шаг индукции.) Из истинности при (предположение индукции) вытекает истинность этого высказывания при , т.е. $A(k)\Rightarrow A(k+1)$ -- истинная импликация.

Пример 1.3.1. Докажем истинность формулы

$\begin{displaymath} \forall\ n:\ 1+2+\ldots+n=\frac{n(n+1)}{2}. \end{displaymath}$

1. (База индукции.) Докажем истинность формулы при .
В левой части высказывания имеем в правой части -- $\displaystyle \frac{1\cdot 2}{2}=1$ .

2. (Шаг индукции.) Предположим, что

$\begin{displaymath} 1+2+\ldots+k=\frac{k(k+1)}{2} \end{displaymath}$

при некотором

. Докажем равенство

$\begin{displaymath} 1+2+\ldots+k+(k+1)=\frac{(k+1)(k+2)}{2}. \end{displaymath}$

Сумма $1+2+\ldots+k+(k+1)$ по предположению индукции равна

, что легко преобразуется к виду

, т.е. к правой части требуемого равенства. Итак, истинность

влечет истинность

. Следовательно, формула

$\begin{displaymath} 1+2+\ldots+n=\frac{n(n+1)}{2} \end{displaymath}$

верна при всех

Задача 1.3.1. Докажите, используя метод математической индукции, истинность следующих высказываний для всех натуральных чисел :

1) $1^2+2^2+\ldots+n^2=n(n+1)(2n+1)/6$ ;
2)формула "бинома Ньютона":

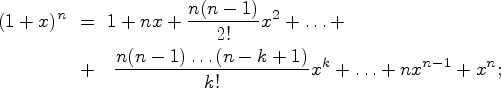
$\begin{eqnarray*} (1+x)^n \!\! &=& \!\! 1+nx+\displaystyle \frac{n(n-1)}{2!}x^2... ...\\ &+&\frac{n(n-1)\ldots(n-k+1)}{k!}x^k+\ldots +nx^{n-1}+x^n; \end{eqnarray*}$

3) $(1+x)^n\ge1+nx$ ,

;
4) $1+2+2^2+2^3+\ldots+2^{n-1}=2^n-1$ ;
5) $(2n)!<2^{2n(n!)^2}$ .

1.4. Элементы теории множеств

Понятия множество, элемент множества, элемент принадлежит множеству -- исходные в математике и не определяются через другие понятия.

Часто множество записывают в виде $\{x\in X:\ A(x)\}$ , где -- предикат, -- некоторое множество из области изменения переменной величины .

Пример 1.4.1. (См. рис. 1.4.1, 1.4.2.)

$A=\{(x,y):y\geq x^2-x\}$ $B=\{(x,y):y\leq x\}$

Рис. 1.4.1 Рис. 1.4.2

Тот факт, что элемент принадлежит множеству , записывают как $a\in A$ . Если элемент не принадлежит множеству , пишут: $a\notin A$ . Для удобства вводится понятие пустого множества, обозначаемого символом $\varnothing$ , как множества, которому не принадлежат никакие элементы.

Множество называется подмножеством множества , если $\left(\forall\ x\right):\ (x\in B)\Rightarrow(x\in A)$ . Это записывают как $B\subset A$ (читается: " включено в ''). Множества и называют равными, если $A\subset B$ и $B\subset A$ , и пишут: .

Из множеств можно строить новые множества с помощью операций $\left(\cup,\ \cap,\ \setminus\ \right)$ :

1. $A\cup B=\{x:(x\in A)\vee(x\in B)\}$ -- объединение множеств и ;

2. $A\cap B=\{x:(x\in A)\wedge(x\in B)\}$ -- пересечение множеств и ;

3. $A\setminus B=\{x:(x\in A)\wedge(x\notin B\}$ -- разность множеств и .

Пример 1.4.2. Пусть множества и -- как в примере 1.4.1. Вот как выглядят множества $A\cup B$ , $A\cap B$ , $A\setminus B$ в этом случае (см. рис. 1.4.3-1.4.5):

Рис. 1.4.3 Рис. 1.4.4 Рис. 1.4.5

Задача 1.4.1. Покажите, что

1) $A\cup(B\cup C)=(A\cup B)\cup C$ ;

2) $A\cap(B\cap C)=(A\cap B)\cap C$ ;

3) $A\cap(B\cup C)=(A\cap B)\cup(A\cap C)$ ;

4) $A\cup(B\cap C)=(A\cup B)\cap(A\cup C$ ).