Последовательность 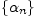 называется
бесконечно малой, если
называется
бесконечно малой, если 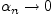 при
при 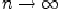 . Развернутое определение:
. Развернутое определение:
Последовательность 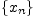 называется
бесконечно большой, если
называется
бесконечно большой, если
Этот факт мы будем
записывать так: 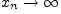 при
при 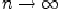 или
или
Функция
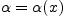 называется
бесконечно малой функцией при
называется
бесконечно малой функцией при 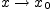 , если
, если
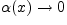 при
при 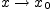 .
.
Функция 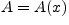 называется
бесконечно большой функцией при
называется
бесконечно большой функцией при 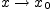 , если
, если
или, в развернутой форме, если для любого 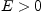 существует
существует 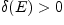 , что для всех
, что для всех
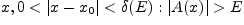 .
.
![]() называется
бесконечно малой, если
называется
бесконечно малой, если ![]() при
при ![]() . Развернутое определение:
. Развернутое определение:
![]()