Основными, неопределяемыми понятиями
в теории действительных чисел являются
натуральные числа
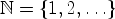
.
Функция 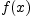 называется
называется 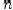 раз
непрерывно дифференцируемой
на некотором промежутке, если на этом промежутке она имеет непрерывные
производные до
раз
непрерывно дифференцируемой
на некотором промежутке, если на этом промежутке она имеет непрерывные
производные до 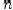 -го порядка включительно.
-го порядка включительно.
Пусть функция 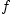 имеет первообразную на некотором промежутке
имеет первообразную на некотором промежутке 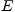 .
Неопределенным интегралом от функции
.
Неопределенным интегралом от функции 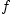 на промежутке
на промежутке 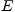 называется совокупность всех первообразных функций для
называется совокупность всех первообразных функций для 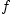 на
на 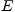 , и он
обозначается
, и он
обозначается
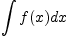 . Поэтому
. Поэтому
где 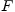 -- одна из первообразных для
-- одна из первообразных для 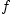 на
на 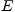 .
.
![]() .
.