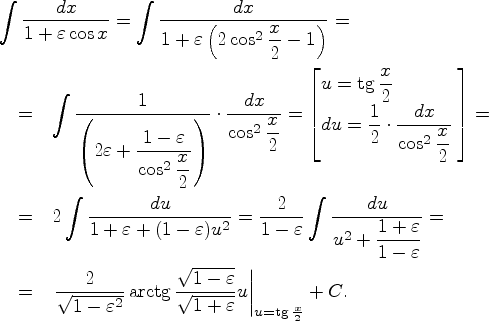8.1. Первообразная, неопределенный интеграл и их свойства
Функция ![]() , определенная на конечном или бесконечном промежутке
, определенная на конечном или бесконечном промежутке
![]() , называется
первообразной функцией, или первообразной, функции
, называется
первообразной функцией, или первообразной, функции ![]() на промежутке
на промежутке ![]() , если она дифференцируема на нем и имеет место
равенство
, если она дифференцируема на нем и имеет место
равенство ![]() для каждого
для каждого ![]() .
.
Пример 8.1.1.
![]() . Первообразной
для этой функции на
. Первообразной
для этой функции на
![]() будет, например,
будет, например, ![]() .
.
Теорема 8.1.1 Если ![]() -- какая-либо первообразная
функции
-- какая-либо первообразная
функции ![]() на промежутке
на промежутке ![]() , то всякая функция вида
, то всякая функция вида
Доказательство.
Пусть ![]() и
и ![]() -- две первообразные для функции
-- две первообразные для функции ![]() на промежутке
на промежутке
![]() , т. е.
, т. е.
![]() и
и
![]()
![]() . Следовательно,
. Следовательно,
![]() на промежутке
на промежутке ![]() .
Рассмотрим функцию
.
Рассмотрим функцию
![]() .
.
Эта функция имеет производную,
всюду равную нулю. Возьмем любые точки
![]() .
Функция
.
Функция ![]() удовлетворяет теореме Лагранжа на отрезке
удовлетворяет теореме Лагранжа на отрезке ![]() (непрерывна на
(непрерывна на
![]() , дифференцируема на
, дифференцируема на ![]() ). Следовательно, по этой
теореме существует
). Следовательно, по этой
теореме существует
![]() такая, что
такая, что
![]() Отсюда следует, что
Отсюда следует, что
![]() на
на ![]() . Следовательно,
. Следовательно,
![]() . Итак, все первообразные для
. Итак, все первообразные для
![]() есть
есть ![]() .
.
Пусть функция ![]() имеет первообразную на некотором промежутке
имеет первообразную на некотором промежутке ![]() .
Неопределенным интегралом от функции
.
Неопределенным интегралом от функции ![]() на промежутке
на промежутке ![]() называется совокупность всех первообразных функций для
называется совокупность всех первообразных функций для ![]() на
на ![]() , и он
обозначается
, и он
обозначается
![]() . Поэтому
. Поэтому
1. Если функция ![]() дифференцируема на промежутке
дифференцируема на промежутке ![]() , то
, то
2. Пусть для функции ![]() существует первообразная на промежутке
существует первообразная на промежутке ![]() ,
тогда
,
тогда
3. Если функции ![]() и
и ![]() имеют первообразные на промежутке
имеют первообразные на промежутке ![]() ,
то функция
,
то функция
![]() тоже имеет первообразную на
тоже имеет первообразную на ![]() ,
и имеет место равенство
,
и имеет место равенство
Доказательства этих свойств следуют из определений производной и неопределенного интеграла.
Исходя из определения неопределенного интеграла, таблицы производных и правил дифференцирования, можно записать следующие равенства, верные на соответствующих промежутках:
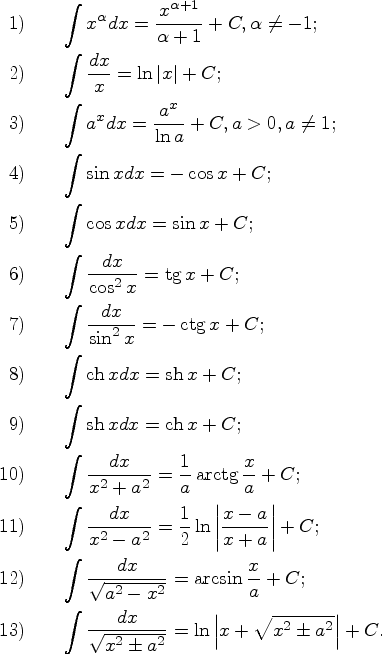
8.2. Интегрирование заменой переменной
Теорема 8.2.1. Пусть функции ![]() и
и ![]() определены на некоторых промежутках так, что имеет смысл сложная функция
определены на некоторых промежутках так, что имеет смысл сложная функция
![]() . Пусть функция
. Пусть функция ![]() имеет первообразную
имеет первообразную
![]() , а
функция
, а
функция ![]() дифференцируема, тогда
функция
дифференцируема, тогда
функция
![]() имеет первообразную
имеет первообразную
![]() .
.
Доказательство. Функции ![]() и
и ![]() определены на одном
промежутке, следовательно, имеет смысл сложная функция
определены на одном
промежутке, следовательно, имеет смысл сложная функция
![]() . По правилу вычисления производной
сложной функции имеем
. По правилу вычисления производной
сложной функции имеем
![$\displaystyle \frac{d}{dx}F\left[\varphi(x)\right]$](../img/img1469.gif) |
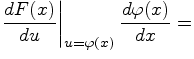 |
||
![$\displaystyle f(u) \Bigl\vert _{u=\varphi(x)}\varphi^{'}(x)=f\left[\varphi(x)\right]\varphi^{'}(x).$](../img/img1472.gif) |
(8.2.1) |
Замечание 8.2.1.
Формула (8.2.1) называется еще формулой интегрирования
подстановкой, так как, учитывая, что
![\begin{displaymath}
\Phi(x)+C=F\left[\varphi(x)\right]+C=
F\left[u\right]\Bigg...
...t _{u=\varphi(x)}+C
=\int f(u)du\Biggr\vert _{u=\varphi(x)},
\end{displaymath}](../img/img1473.gif)
![\begin{displaymath}
\int f\left[\varphi(x)\right]\varphi^{'}(x)dx=
\left.\int f(u)du\right\vert _{u=\varphi(x)}. \eqno(8.2.2)
\end{displaymath}](../img/img1475.gif)
Пример 8.2.1
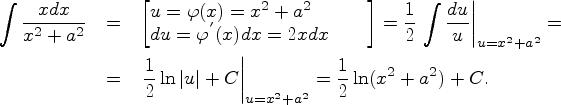
![\begin{displaymath}
\int f(u)du=
\left.\int f\left[\varphi(x)\right]\varphi^{'}(x)dx
\right\vert _{x=\varphi^{-1}(u)}.
\eqno(8.2.3)
\end{displaymath}](../img/img1481.gif)
Таким образом, вычисление интеграла
![]() с помощью
замены
переменной
с помощью
замены
переменной ![]() на переменную
на переменную
![]() сводится к вычислению интеграла
сводится к вычислению интеграла
![]() и подстановке затем вместо переменной
и подстановке затем вместо переменной
![]() функции
функции
![]() .
.
Пример 8.2.2
![\begin{eqnarray*}
\lefteqn{\int \sqrt{1-u^2}du =
\left[\parbox{35mm}{$u = \varp...
...}=\\ [5pt]
&=&\frac{1}{2}\arcsin u+\frac{1}{2}u\sqrt{1-u^2}+C.
\end{eqnarray*}](../img/img1484.gif)
Теорема 8.3.1. Если функции ![]() и
и ![]() дифференцируемы на некотором промежутке
дифференцируемы на некотором промежутке ![]() и существует первообразная для
и существует первообразная для
![]() на
на ![]() , то существует первообразная для
, то существует первообразная для
![]() на
на ![]() и имеет место формула
и имеет место формула
Формула интегрирования по частям (8.3.1) следует из равенства
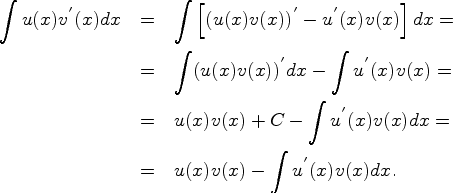
Замечание 8.3.1. Учитывая равенства
![]() ,
формулу интегрирования по частям (8.3.1) можно записать в таком виде:
,
формулу интегрирования по частям (8.3.1) можно записать в таком виде:
Пример 8.3.1
![\begin{eqnarray*}
\int x\sin xdx =\left[\parbox{3cm}{$u(x)=x$\\ $dv(x)=\sin xdx...
...cos x$}\right]&=&-x\cos x+\int\cos xdx=\\
&=&-x\cos x+\sin x+C.
\end{eqnarray*}](../img/img1495.gif)
Пример 8.3.2
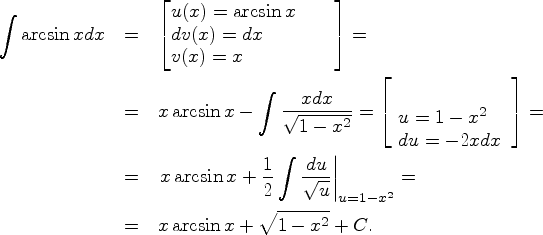
Пример 8.3.3
8.4. Интегралы от рациональных функций
Если рациональная дробь с действительными коэффициентами
Обсудим интегралы от простых дробей:
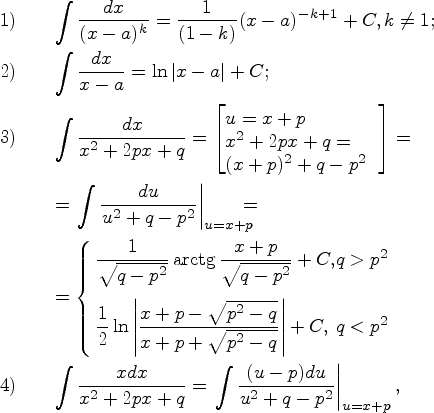
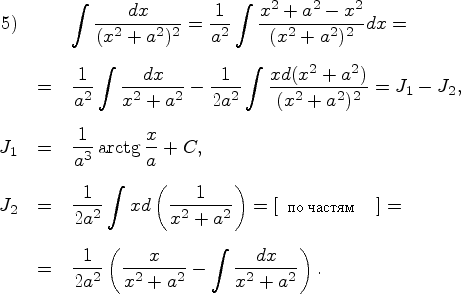
Пример 8.4.1. Пусть
![]()