Последовательность
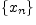 назовем
последовательностью Коши или
фундаментальной, если
назовем
последовательностью Коши или
фундаментальной, если
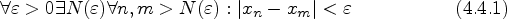
.
Соответствие 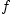 между элементами множеств
между элементами множеств 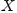 и
и 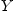 называется
функцией, если любому элементу
называется
функцией, если любому элементу 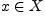 поставлен в соответствие единственный элемент
поставлен в соответствие единственный элемент 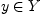 (это записывается следующим образом:
(это записывается следующим образом: 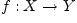 или
или
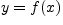 ).
).
Функция 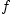 называется
непрерывной в точке
называется
непрерывной в точке 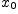 , если существует предел функции
, если существует предел функции 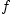 при
при 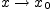 , и он равен ее значению в точке
, и он равен ее значению в точке
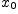 , т. е.
, т. е.
Функция 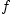 называется
непрерывной в точке
называется
непрерывной в точке
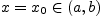 по Коши,
если она определена
в
по Коши,
если она определена
в 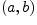 и для любого
и для любого
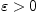 существует
существует 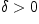 такое,
что для всех
такое,
что для всех
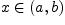 и
и
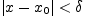 выполняется неравенство
выполняется неравенство
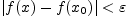 .
.
Функция 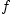 называется
непрерывной в точке
называется
непрерывной в точке
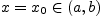 по Гейне,
если она определена
в
по Гейне,
если она определена
в 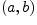 и для любой последовательности
и для любой последовательности
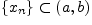 такой, что
такой, что
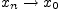 , выполняется
, выполняется
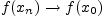 .
.
Функция 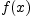 непрерывна на отрезке
непрерывна на отрезке
![$[a,b]$](../img/img785.gif) , если она
непрерывна во всех точках интервала
, если она
непрерывна во всех точках интервала 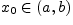 и непрерывна справа
в точке
и непрерывна справа
в точке 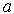 и слева в точке
и слева в точке 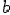 .
.
Функция 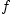 равномерно непрерывна на промежутке
равномерно непрерывна на промежутке
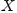 , если
, если
Функция 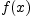 называется
строго возрастающей на
множестве
называется
строго возрастающей на
множестве 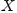 ,
если для всех
,
если для всех 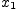 и
и 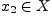
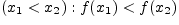 .
Аналогично определяется строго убывающая функция. Строго убывающие и строго возрастающие функции называются
строго монотонными.
.
Аналогично определяется строго убывающая функция. Строго убывающие и строго возрастающие функции называются
строго монотонными.
![]() назовем
последовательностью Коши или
фундаментальной, если
назовем
последовательностью Коши или
фундаментальной, если
![]() .
.