6.1. Точки непрерывности и разрыва функции
Предположим, что функция ![]() определена в некоторой окрестности точки
определена в некоторой окрестности точки ![]() Функция
Функция ![]() называется
непрерывной в точке
называется
непрерывной в точке ![]() , если существует предел функции
, если существует предел функции ![]() при
при ![]() , и он равен ее значению в точке
, и он равен ее значению в точке
![]() , т. е.
, т. е.
Можно записать развернутое определение непрерывности
функции в точке, если
воспользоваться определением предела функции по Коши или Гейне.
Функция ![]() называется непрерывной в точке
называется непрерывной в точке
![]() по Коши,
если она определена
в
по Коши,
если она определена
в ![]() и для любого
и для любого
![]() существует
существует ![]() такое,
что для всех
такое,
что для всех
![]() и
и
![]() выполняется неравенство
выполняется неравенство
![]() .
.
Функция ![]() называется непрерывной в точке
называется непрерывной в точке
![]() по Гейне,
если она определена
в
по Гейне,
если она определена
в ![]() и для любой последовательности
и для любой последовательности
![]() такой, что
такой, что
![]() , выполняется
, выполняется
![]() .
.
Пример 6.1.1. ![]() непрерывна в любой точке,
так как
если
непрерывна в любой точке,
так как
если ![]() , то
, то
![]() .
.
Точка ![]() называется
точкой разрыва
функции
называется
точкой разрыва
функции ![]() ,
если функция определена на интервале
,
если функция определена на интервале ![]() , а в точке
, а в точке
![]() не определена или определена и в точке
не определена или определена и в точке ![]() , но не является непрерывной в ней.
, но не является непрерывной в ней.
Предположим, что точка ![]() -- точка разрыва функции
-- точка разрыва функции ![]() . Точка
. Точка ![]() называется точкой
разрыва первого рода функции
называется точкой
разрыва первого рода функции ![]() , если у функции
, если у функции ![]() существуют
в этой точке конечные односторонние пределы.
В противном случае точка
существуют
в этой точке конечные односторонние пределы.
В противном случае точка ![]() называется точкой разрыва второго рода функции
называется точкой разрыва второго рода функции ![]() .
.
Приведем схематически все возможные варианты точек разрыва функции первого рода (см. рис. 6.1.1).
Пример 6.1.2. Функция
Пример 6.1.3. Для функции
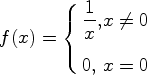
Исходя из свойств предела, можно доказать следующую теорему.
Теорема 6.1.1.
Если функции ![]() и
и
![]() непрерывны в точке
непрерывны в точке ![]() , то непрерывны в точке
, то непрерывны в точке
![]() и функции
и функции ![]()
![]() Если, кроме того,
Если, кроме того, ![]() , то функция
, то функция ![]() тоже непрерывна в точке
тоже непрерывна в точке ![]() .
.
Пример 6.1.4.
![]() непрерывна в любой точке
непрерывна в любой точке ![]() .
.
Примеры непрерывных функций:
![]() непрерывна в
непрерывна в ![]() (в каждой точке множества
(в каждой точке множества ![]() );
);
![]() непрерывна в
непрерывна в ![]() ;
;
![]() непрерывна в
непрерывна в ![]() ;
;
![]() ,
, ![]() непрерывны в
непрерывны в ![]() , так как (см. (6.1.3))
, так как (см. (6.1.3))
Первый замечательный предел.
Докажем, что имеет место следующее равенство:
Теорема 6.1.2. Если функция
![]() непрерывна в точке
непрерывна в точке ![]() ,
а функция
,
а функция ![]() непрерывна в точке
непрерывна в точке ![]() , где
, где
![]() ,
то сложная функция
,
то сложная функция
![]() непрерывна в точке
непрерывна в точке
![]() .
.
Доказательство. Пусть ![]() . Тогда в силу непрерывности
в точке
. Тогда в силу непрерывности
в точке ![]() функции
функции ![]() последовательность
последовательность
![]()
сходится к
![]() .
Но тогда, в силу непрерывности уже функции
.
Но тогда, в силу непрерывности уже функции ![]() в точке
в точке ![]() ,
последовательность
,
последовательность
![]() сходится к
сходится к
![]() .
Итак, из определения Гейне следует, что функция
.
Итак, из определения Гейне следует, что функция
![]() непрерывна в точке
непрерывна в точке ![]() .
.
Замечание 6.1.1.
Если считать, что существуют пределы
![]() при
при ![]() и
и
![]() при
при ![]() , то в теореме 6.1.2 доказано, что
, то в теореме 6.1.2 доказано, что
Пример 6.1.5.
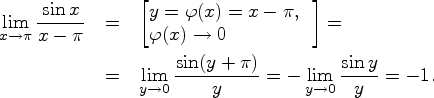
6.2. Свойства функций, непрерывных на отрезке
Напомним, что функция ![]() непрерывна на отрезке
непрерывна на отрезке
![]() , если она
непрерывна во всех точках интервала
, если она
непрерывна во всех точках интервала ![]() и непрерывна справа
в точке
и непрерывна справа
в точке ![]() и слева в точке
и слева в точке ![]() .
.
Для таких функций имеет место ряд важных теорем.
Теорема 6.2.1 (первая теорема Вейерштрасса).
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() ,
то она ограничена
на нем.
,
то она ограничена
на нем.
Необходимо доказать, что существует ![]() , что для всех
, что для всех
![]() выполняется
выполняется
![]() .
.
Доказательство (от противного).
Пусть для всякого ![]() найдется
такая точка
найдется
такая точка
![]() , что
, что
![]() :
:
для ![]() найдется
найдется
![]() ;
;
для ![]() найдется
найдется
![]() и т. д.,
и т. д.,
. . . . . . . .
для ![]() найдется
найдется
![]() и т. д.,
и т. д.,
. . . . . . . .
Итак, построена последовательность
![]() такая, что для всех
такая, что для всех ![]() :
: ![]() . Ясно, что
. Ясно, что
![]() .
Последовательность
.
Последовательность
![]() , т. е. ограничена. Следовательно,
по теореме Больцано - Вейерштрасса,
существует подпоследовательность
, т. е. ограничена. Следовательно,
по теореме Больцано - Вейерштрасса,
существует подпоследовательность
![]() такая,
что
такая,
что
![]() . Так как функция
. Так как функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() , она непрерывна и в точке
, она непрерывна и в точке
![]() .
Итак, имеем
.
Итак, имеем
![]() , но по построению
, но по построению
![]() ,
что является противоречием.
,
что является противоречием.
Пример 6.2.1. На интервале теорема, вообще говоря,
неверна.
Функция ![]() непрерывна на
непрерывна на ![]() , но не ограничена на нем.
, но не ограничена на нем.
Теорема 6.2.2 (вторая теорема Вейерштрасса).
Непрерывная функция ![]() на отрезке
на отрезке ![]() достигает в некоторых точках
отрезка
достигает в некоторых точках
отрезка ![]() своих точных верхней и нижней границ, т. е.
существуют
своих точных верхней и нижней границ, т. е.
существуют
![]() такие, что
такие, что
Доказательство. Докажем существование точки максимума функции ![]() , т.е. точки
, т.е. точки
![]() , в которой значение функции равно точной верхней грани множества значений функции
, в которой значение функции равно точной верхней грани множества значений функции
![]() . По предыдущей теореме 6.2.1 непрерывная на отрезке
. По предыдущей теореме 6.2.1 непрерывная на отрезке ![]() функция
функция ![]() является ограниченной на этом отрезке, следовательно, ограничена сверху,
например, числом
является ограниченной на этом отрезке, следовательно, ограничена сверху,
например, числом ![]() , т. е. для всех
, т. е. для всех
![]() .
Тогда существует точная верхняя граница
.
Тогда существует точная верхняя граница ![]() множества значений функции
множества значений функции ![]() на отрезке
на отрезке ![]()
![]() ,
т.е. такое число
,
т.е. такое число ![]() , что
, что
1) для всех
![]() ;
;
2) для любого ![]() существует точка
существует точка
![]()
![]() .
.
Возьмем последовательные значения
![]()
Тогда построена последовательность
![]() . Эта последовательность ограничена.
Следовательно, по теореме Больцано - Вейерштрасса
из нее можно выделить подпоследовательность
. Эта последовательность ограничена.
Следовательно, по теореме Больцано - Вейерштрасса
из нее можно выделить подпоследовательность
![]() такую, что
такую, что
![]() .
Функция
.
Функция ![]() непрерывна в точке
непрерывна в точке ![]() .
.
Следовательно,
![]() , но, с другой стороны, для всех
, но, с другой стороны, для всех ![]() выполняется
выполняется
![]() .
В силу свойства 3.2.5 сходящихся последовательностей заключаем, что
.
В силу свойства 3.2.5 сходящихся последовательностей заключаем, что
![]() . Итак,
. Итак,
![]() .
.
Замечание 6.2.1. Если функция разрывна,
то теорема 6.2.2, вообще
говоря, неверна. Например,
![]() ,
, ![]() (см. рис. 6.2.1).
Значение, равное
(см. рис. 6.2.1).
Значение, равное ![]() , функцией не достигается.
, функцией не достигается.
Теорема 6.2.3. Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() ,
ее значения на концах отрезка
,
ее значения на концах отрезка ![]() и
и ![]() не равны нулю
и имеют разные знаки, то на интервале
не равны нулю
и имеют разные знаки, то на интервале ![]() имеется по крайней мере
одна точка
имеется по крайней мере
одна точка ![]() такая, что
такая, что ![]() .
.
Доказательство (метод Больцано деления отрезка пополам).
Пусть ![]() (см. рис. 6.2.3).
(см. рис. 6.2.3).
Обозначим отрезок
![]() .
Разделим его пополам.
Если в середине отрезка
.
Разделим его пополам.
Если в середине отрезка ![]() функция равна нулю, то все доказано.
Если нет,
то обозначим за
функция равна нулю, то все доказано.
Если нет,
то обозначим за
![]() ту из половин отрезка
ту из половин отрезка ![]() ,
на концах которой
функция
,
на концах которой
функция
![]() имеет разные знаки:
имеет разные знаки:
![]() .
Разделим отрезок
.
Разделим отрезок ![]() пополам. Если в середине отрезка
пополам. Если в середине отрезка ![]() функция равна нулю, то все доказано.
Если нет, то обозначим за
функция равна нулю, то все доказано.
Если нет, то обозначим за
![]() ту из половин отрезка
ту из половин отрезка ![]() ,
на концах которой функция
,
на концах которой функция
![]() имеет разные знаки:
имеет разные знаки:
![]() .
Рассуждая таким образом, мы либо на
каком-то шаге получим точку, в которой функция обращается в нуль,
и все доказано,
либо построим систему вложенных отрезков,
длины которых стремятся к нулю, и для всех
.
Рассуждая таким образом, мы либо на
каком-то шаге получим точку, в которой функция обращается в нуль,
и все доказано,
либо построим систему вложенных отрезков,
длины которых стремятся к нулю, и для всех
![]() выполняются неравенства
выполняются неравенства
![]() .
Следовательно, по теореме Кантора
существует точка
.
Следовательно, по теореме Кантора
существует точка ![]() , принадлежащая всем отрезкам
, принадлежащая всем отрезкам ![]() .
Поэтому
.
Поэтому
![]() и
и
![]() . Тогда, с одной
стороны,
. Тогда, с одной
стороны,
Теорема 6.2.4. Если функция ![]() непрерывна на отрезке
непрерывна на отрезке
![]() , причем
, причем ![]() , и
, и ![]() -- произвольное число такое, что
-- произвольное число такое, что
![]() , то на интервале
, то на интервале
![]() найдется по крайней мере одна точка
найдется по крайней мере одна точка ![]() ,
в которой
,
в которой ![]()
![]() т. е. непрерывная на отрезке функция принимает все
промежуточные значения
между ее значениями на концах отрезка
т. е. непрерывная на отрезке функция принимает все
промежуточные значения
между ее значениями на концах отрезка![]() .
.
Доказательство. Рассмотрим функцию ![]() ,
где
,
где ![]() . Функция
. Функция
![]() непрерывна на отрезке
непрерывна на отрезке ![]() , и
, и
![]() ,
,
![]() . Следовательно, по теореме 6.2.3
существует точка
. Следовательно, по теореме 6.2.3
существует точка
![]() . Отсюда,
. Отсюда, ![]() .
.
Замечание 6.2.2. Если функция разрывна,
то теорема, вообще
говоря, неверна. Например, можно взять функцию
![]() .
Числовые значения из промежутка
.
Числовые значения из промежутка ![]() этой функцией не принимаются (см. рис. 6.2.2).
этой функцией не принимаются (см. рис. 6.2.2).
6.3. Равномерно непрерывные функции
Напомним ряд определений.
Функция ![]() непрерывна в точке
непрерывна в точке ![]() из промежутка
из промежутка ![]() ,
если
,
если
Функция ![]() непрерывна на промежутке
непрерывна на промежутке ![]() , если
, если
Функция ![]() равномерно непрерывна на промежутке
равномерно непрерывна на промежутке
![]() , если
, если
В случае равномерной непрерывности функции ![]() на
промежутке
на
промежутке ![]() параметр
параметр ![]() зависит только от величины
зависит только от величины ![]() ,
но не от расположения
точки
,
но не от расположения
точки ![]() на промежутке
на промежутке ![]() . Поэтому точки
. Поэтому точки
![]() и
и ![]() можно считать
равноправными, и в определении они обозначены как
можно считать
равноправными, и в определении они обозначены как ![]() и
и
![]() . Очевидно, равномерная непрерывность
. Очевидно, равномерная непрерывность ![]() на
на ![]() влечет непрерывность
влечет непрерывность ![]() на
на ![]() .
Механически свойство равномерной непрерывности
функции на промежутке можно представить как возможность при любом
.
Механически свойство равномерной непрерывности
функции на промежутке можно представить как возможность при любом
![]() найти такую длину трубки
найти такую длину трубки ![]() , что ее можно протянуть через график функции вдоль
всего промежутка так, чтобы ось трубки была все время параллельна оси
, что ее можно протянуть через график функции вдоль
всего промежутка так, чтобы ось трубки была все время параллельна оси ![]() (см. рис. 6.3.1).
Видно, что чем "круче" график функции, тем меньше длина
трубки.
(см. рис. 6.3.1).
Видно, что чем "круче" график функции, тем меньше длина
трубки.
Очевидно, что функция ![]() равномерно непрерывна на всей числовой
оси, а неограниченные функции на конечном промежутке не могут быть на нем
равномерно непрерывны. Например, такова функция
равномерно непрерывна на всей числовой
оси, а неограниченные функции на конечном промежутке не могут быть на нем
равномерно непрерывны. Например, такова функция
![]() на промежутке
на промежутке
![]() . Но существуют и ограниченные функции, не являющиеся равномерно
непрерывными на конечном промежутке. Например, функция
. Но существуют и ограниченные функции, не являющиеся равномерно
непрерывными на конечном промежутке. Например, функция
![]() не является равномерно непрерывной на промежутке
не является равномерно непрерывной на промежутке ![]() . Действительно, достаточно взять
. Действительно, достаточно взять
![]() , тогда для любого
, тогда для любого ![]() найдутся точки вида
найдутся точки вида
![]() и
и
![]() такие, что
такие, что
![]() и
и
Теорема 6.3.1 (Кантор). Непрерывная на отрезке
![]() функция
функция ![]() равномерно непрерывна на этом отрезке.
равномерно непрерывна на этом отрезке.
Доказательство (от противного). Пусть для некоторого ![]() и любого
и любого ![]() найдутся точки
найдутся точки
![]() ,
такие, что
,
такие, что
![]() .
Для
.
Для ![]() найдутся
найдутся
![]()
Тогда по свойству 3.2.5 сходящихся последовательностей получим, что
![]() при
при ![]() . Итак, последовательности
. Итак, последовательности
![]() и
и
![]() сходятся к одной точке
сходятся к одной точке ![]() . Функция
. Функция ![]() непрерывна в точке
непрерывна в точке
![]() и, следовательно, последовательности
и, следовательно, последовательности
![]() сходятся к одному пределу
сходятся к одному пределу ![]() ,
что невозможно, так как их разность
,
что невозможно, так как их разность
![]() не стремится к нулю.
не стремится к нулю.
6.4. Монотонные функции. Существование
обратных функций
Пусть дана функция
![]() .
Она отображает множество
.
Она отображает множество ![]() на множество
на множество ![]() , т. е.
, т. е.
![]() . Это означает, что для любого
. Это означает, что для любого ![]() множество
множество
![]() . Обратное соответствие
. Обратное соответствие
![]() определено на любом элементе
определено на любом элементе ![]() ,
однако обратное соответствие может не
быть функцией, т. е. однозначным соответствием.
Выясним некоторые достаточные
условия существования обратной функции.
,
однако обратное соответствие может не
быть функцией, т. е. однозначным соответствием.
Выясним некоторые достаточные
условия существования обратной функции.
Функция ![]() называется строго возрастающей на
множестве
называется строго возрастающей на
множестве ![]() ,
если для всех
,
если для всех ![]() и
и ![]()
![]() .
Аналогично определяется
строго убывающая функция. Строго убывающие и строго возрастающие функции называются
строго монотонными.
.
Аналогично определяется
строго убывающая функция. Строго убывающие и строго возрастающие функции называются
строго монотонными.
Теорема 6.4.1 Если функция
![]() и строго монотонная на множестве
и строго монотонная на множестве ![]() , то обратное
соответствие
, то обратное
соответствие
![]() однозначное,
т. е. будет обратной функцией, и тоже строго монотонное.
однозначное,
т. е. будет обратной функцией, и тоже строго монотонное.
Доказательство. Положим, для определенности,
что функция
![]() строго монотонно возрастает на
строго монотонно возрастает на ![]() .
Возьмем любое
.
Возьмем любое ![]() . Так как по условию
теоремы прямая функция отображает
. Так как по условию
теоремы прямая функция отображает ![]() на
на ![]() ,
то полный прообраз элемента
,
то полный прообраз элемента
![]() не пуст, т. е.
не пуст, т. е.
![]() .
Если предположить, что
.
Если предположить, что
![]() состоит более чем из одного элемента,
то получим противоречие.
Действительно, пусть
состоит более чем из одного элемента,
то получим противоречие.
Действительно, пусть
![]() .
Тогда, если
.
Тогда, если ![]() , то
по условию строгого монотонного возрастания функции
, то
по условию строгого монотонного возрастания функции ![]() справедливо неравенство
справедливо неравенство
![]() , но это противоречит тому, что
, но это противоречит тому, что
![]() .
Если
.
Если ![]() , получим аналогичное противоречие. Следовательно,
, получим аналогичное противоречие. Следовательно,
![]() состоит только
из одного элемента, и поэтому соответствие
состоит только
из одного элемента, и поэтому соответствие
![]() есть обратная функция.
есть обратная функция.
Функция ![]() -- строго монотонно возрастающая на
-- строго монотонно возрастающая на ![]() Действительно,
пусть
Действительно,
пусть ![]() и
и
![]() ,
,
![]() , тогда если
, тогда если ![]() ,
то
,
то
![]() ,
а у нас
,
а у нас ![]() ; если
; если ![]() ,
то
,
то
![]() ,
а у нас
,
а у нас ![]() .
Следовательно,
.
Следовательно,
![]() ,
т. е. функция
,
т. е. функция ![]() строго монотонно возрастает на
строго монотонно возрастает на ![]() .
.
Теорема 6.4.2. Пусть функция
![]() определена, непрерывна и
строго возрастает на отрезке
определена, непрерывна и
строго возрастает на отрезке ![]()
![]()
![]() .
Тогда
.
Тогда
![]() , и
обратная функция
, и
обратная функция ![]() определена,
непрерывна и строго возрастает на отрезке
определена,
непрерывна и строго возрастает на отрезке ![]() .
.
Доказательство. Докажем сначала, что
![]() .
.
Пусть ![]() . Если
. Если ![]() или
или ![]() , то
, то ![]() . Если
. Если ![]() ,
то по теореме 6.2.4
найдется
,
то по теореме 6.2.4
найдется ![]() такая, что
такая, что ![]() , т. е.
, т. е.
![]() .
.
Пусть ![]() , тогда найдется
, тогда найдется ![]() такая, что
такая, что ![]() .
Следовательно, в силу строгого возрастания функции
.
Следовательно, в силу строгого возрастания функции ![]() на отрезке
на отрезке ![]() имеем:
имеем:
![]() . Таким образом,
. Таким образом,
![]() .
.
Итак,
![]() и
строго возрастает,
следовательно, по теореме 6.4.1 существует обратная функция
и
строго возрастает,
следовательно, по теореме 6.4.1 существует обратная функция
![]() , и она строго
возрастает на
, и она строго
возрастает на ![]() .
.
Докажем теперь непрерывность функции ![]() на отрезке
на отрезке
![]() .
Рассмотрим любое
.
Рассмотрим любое ![]() и
любую последовательность
и
любую последовательность
![]() , сходящуюся к
, сходящуюся к ![]() . Обозначим
. Обозначим
![]()
![]() . Надо доказать,
что
. Надо доказать,
что
![]() . Предположим противное. Тогда из условия
. Предположим противное. Тогда из условия
![]() следует, что существует ее подпоследовательность
следует, что существует ее подпоследовательность
![]() и
и ![]() . Из непрерывности
функции
. Из непрерывности
функции ![]() в точке
в точке ![]() следует сходимость
следует сходимость
![]() к
к
![]() . Но
. Но
![]() ,
а это дает противоречие.
,
а это дает противоречие.
Незначительно изменяя приведенные выше рассуждения, можно доказать следующий аналог предыдущей теоремы.
Теорема 6.4.3. Пусть функция ![]() непрерывна и строго монотонно
возрастает на интервале
непрерывна и строго монотонно
возрастает на интервале
![]() и
и
![]()
![]() .
.
Тогда образ интервала
![]() есть интервал
есть интервал
![]() , и обратная функция
, и обратная функция ![]() существует, непрерывна
и строго монотонно возрастает на интервале
существует, непрерывна
и строго монотонно возрастает на интервале
![]() .
.
Теорема справедлива на ![]() .
.
Пример 6.4.1. Известно, что функция
![]() строго монотонна и непрерывна
на отрезке
строго монотонна и непрерывна
на отрезке
![]() . Тогда по теореме 6.4.2 существует
обратная к ней функция на
отрезке
. Тогда по теореме 6.4.2 существует
обратная к ней функция на
отрезке ![]() , и она непрерывна и строго монотонно
возрастает; это известная функция
, и она непрерывна и строго монотонно
возрастает; это известная функция
![]() .
.
Пример 6.4.2.
![]() .
Эта функция определена,
непрерывна и строго возрастает на луче
.
Эта функция определена,
непрерывна и строго возрастает на луче ![]() .
По теореме 6.4.3
для нее существует обратная функция
.
По теореме 6.4.3
для нее существует обратная функция
Напомним свойства функции
![]() :
:
1)
![]() ;
;
2) если ![]() , то
, то
![]() для любого
для любого ![]() ;
;
3)
![]() ;
;
4)
![]() :
последовательность
:
последовательность
![]() фундаментальна.
фундаментальна.
Докажем свойство 3. Известно, что
Докажем свойство 4. Возьмем любое ![]() и любую
последовательность
и любую
последовательность
![]() . Тогда последовательность
. Тогда последовательность
![]() ограничена,
т. е. существует число
ограничена,
т. е. существует число ![]() такое, что
такое, что
![]() .
Следовательно,
.
Следовательно,
![]() , т. е. последовательность
, т. е. последовательность ![]() ограничена сверху. Докажем, что последовательность
ограничена сверху. Докажем, что последовательность
![]() фундаментальна.
Возьмем любое
фундаментальна.
Возьмем любое
![]() , тогда по свойству 3 существует
, тогда по свойству 3 существует ![]() такое,
что для любого
такое,
что для любого ![]() со свойством
со свойством ![]() выполняется неравенство
выполняется неравенство
![]() .
В силу фундаментальности последовательности
.
В силу фундаментальности последовательности ![]() для найденного
для найденного
![]() существует номер
существует номер ![]() такой, что
для всех
такой, что
для всех ![]() выполняется неравенство
выполняется неравенство
![]() .
Поэтому
.
Поэтому
![]() .
.
Исходя из этого, можно дать такое определение показательной функции
![]() :
:
Свойства функции ![]() на
на
![]() :
:
1)
![]() ;
;
2)
![]() ;
;
3) ![]() ;
;
4) функция ![]() строго
монотонно возрастает на
строго
монотонно возрастает на
![]() ;
;
5)
![]() ;
;
6) функция ![]() непрерывна на
непрерывна на
![]() ;
;
7)
![]() ,
,
![]() .
.
Свойство
6 следует из свойства 5 и равенства
Поскольку функция
![]() строго
возрастает и непрерывна на
строго
возрастает и непрерывна на
![]() и
и
![]() , то по
теореме 6.4.3 существует
обратная к ней функция
, то по
теореме 6.4.3 существует
обратная к ней функция ![]() , и она строго
возрастает на интервале
, и она строго
возрастает на интервале
![]() . Это известная логарифмическая функция
. Это известная логарифмическая функция ![]() .
.
Свойства функции
![]() :
:
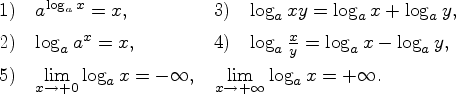
По определению считаем
![]() . Эта функция непрерывна на
. Эта функция непрерывна на ![]() , строго
возрастает.
, строго
возрастает.
Докажем, что справедливы равенства
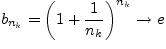 . Сначала докажем,
что
. Сначала докажем,
что
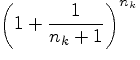 |
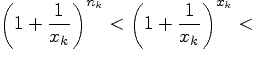 |
||
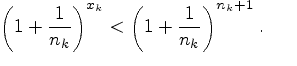 |
(6.5.2) |
Левые и правые части неравенств (6.5.2) при
![]() стремятся к
числу
стремятся к
числу ![]() , следовательно, и
, следовательно, и
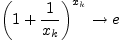 .
Аналогично, для
.
Аналогично, для ![]() .
Для случая
.
Для случая
Как следствие второго замечательного предела имеют место следующие равенства:
В силу непрерывности функции ![]() в точке
в точке ![]()
Для доказательства второго
равенства (6.5.3) рассмотрим функцию
![]() , строго
возрастающую и
непрерывную на отрезке
, строго
возрастающую и
непрерывную на отрезке
![]() . Следовательно,
по теореме 6.4.2
существует обратная к ней функция
. Следовательно,
по теореме 6.4.2
существует обратная к ней функция
![]() , которая строго
возрастает и непрерывна на отрезке
, которая строго
возрастает и непрерывна на отрезке
![]() . Функция
. Функция
![]() имеет предел при
имеет предел при ![]() ,
следовательно, и сложная функция (см. замечание 6.1.1)
,
следовательно, и сложная функция (см. замечание 6.1.1)
Если существуют
![]() ,
,
![]() -- конечный, то из непрерывности
функций
-- конечный, то из непрерывности
функций ![]() и
и ![]() следует, что
следует, что
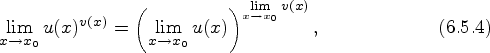
Если
непосредственная подстановка пределов в выражение
![]() приводит к
неопределенности вида
приводит к
неопределенности вида
![]() , то следует
поступить следующим
образом. Необходимо рассмотреть выражение
, то следует
поступить следующим
образом. Необходимо рассмотреть выражение
![]() , перейти в этом
выражении к пределу и затем, потенцируя по основанию
, перейти в этом
выражении к пределу и затем, потенцируя по основанию
![]() , вычислить указанный предел.
, вычислить указанный предел.
Пример 6.5.1. Найдем предел
1)
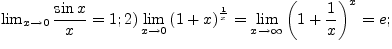
3)
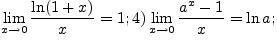
5)
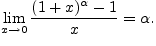
Доказательство последних двух соотношений следует из
равенств
![]() и
и
![]() .
.
6.6. Эквивалентность, порядок функции в точке
При вычислении пределов непосредственное применение замечательных пределов нередко приводит к довольно громоздким выкладкам. Рассмотрим несколько приемов и понятий, упрощающих вычисления.
Функции ![]() и
и ![]() называются эквивалентными
в точке
называются эквивалентными
в точке ![]() (или при
(или при ![]() )
)
![]() ,
если они
определены в окрестности точки
,
если они
определены в окрестности точки ![]() , отличны в ней от
нуля и
, отличны в ней от
нуля и
Пример 6.6.1
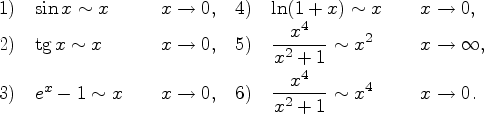
Функция ![]() есть о-малое от функции
есть о-малое от функции
![]() при
при ![]()
![]() , если существует функция
, если существует функция
![]() со свойством
со свойством
![]() при
при ![]() такая, что
такая, что
![]() .
.
Пример 6.6.2
1) ![]() при
при ![]() , так как
, так как
![]() ;
;
2) ![]() при
при ![]() , так как
, так как
3) ![]() при
при
![]() для любого натурального
для любого натурального ![]() , т. е.
, т. е.
4) ![]() при
при
![]() .
Действительно,
.
Действительно,
![\begin{displaymath}
\lim_{x\to+\infty}\frac{\ln^kx}{x}=\left[\parbox{3cm}
{зам...
... x\to+\infty$ }\right]
=\lim_{y\to+\infty}\frac{y^k}{e^y}=0.
\end{displaymath}](../img/img1072.gif)
Теорема 6.6.1. Для того чтобы функции
![]() и
и ![]() ,
отличные от нуля в выколотой окрестности точки
,
отличные от нуля в выколотой окрестности точки ![]() ,
были эквивалентными при
,
были эквивалентными при ![]() необходимо и
достаточно, чтобы
при
необходимо и
достаточно, чтобы
при ![]() выполнялось соотношение
выполнялось соотношение
Доказательство.
Необходимость.
Из эквивалентности
функций ![]() и
и ![]() в точке
в точке ![]() следует, что
следует, что
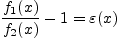 есть бесконечно малая функция.
Отсюда вытекает требуемое равенство (6.6.1).
есть бесконечно малая функция.
Отсюда вытекает требуемое равенство (6.6.1).
Достаточность доказывается аналогично.
Выпишем таблицу эквивалентностей в точке ![]() некоторых классических бесконечно малых функций:
некоторых классических бесконечно малых функций:
1) ![]() ,
, ![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() ;
;
3)
![]() ;
;
4)
![]() ,
,
![]() ;
;
5)
![]() ,
,
![]() .
.
Для нахождения пределов бывает удобно заменять множители на эквивалентные им функции.
Теорема 6.7.2. Пусть ![]() при
при
![]() , и
функция
, и
функция ![]() отлична от нуля в некоторой окрестности
точки
отлична от нуля в некоторой окрестности
точки ![]() .
Тогда, если существует один из пределов
.
Тогда, если существует один из пределов
Доказательство. Предположим, что существует второй предел. Тогда
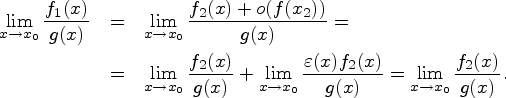
Пример 6.6.3
![\begin{displaymath}
1)\ \lim_{x\to0}\frac{\root 3\of{1+2x}-1}
{\root 4\of{1-3x...
...
\phantom{i} \root 4\of{1-3x}-1\sim-3x^\frac{1}{4}$}\right];
\end{displaymath}](../img/img1088.gif)
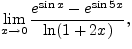
Здесь использовались некоторые из свойств ![]() -малого:
-малого:
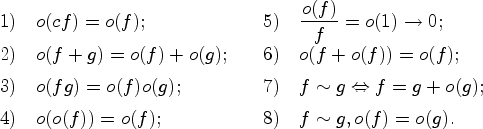
Пример 6.6.4